Vektorielle Betrachtung

Der Geschwindigkeitsvektor ist wie bei jeder Bewegung tangential zur Bahnkurve, also hier tangential zum Kreis. Damit steht er senkrecht auf dem Radiusvektor. Er zeigt in Bewegungsrichtung.

${\displaystyle {\vec {v}}={\underset {\Delta t\rightarrow 0}{\lim }}{\frac {\Delta {\vec {r}}}{\Delta t}}\Rightarrow {\vec {r}}\perp {\vec {v}}}$

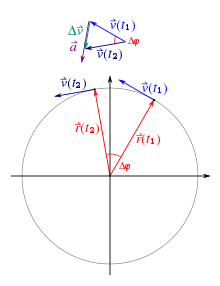
Anhand der vektoriellen Betrachtung lässt sich auch die erforderliche Beschleunigung für eine Richtungsänderung ohne Betragsänderung der Geschwindigkeit ermitteln. Analog dem Vorgehen bei der Betrachtung des Geschwindigkeitsvektors erfolgt die Herleitung der Beschleunigung. Der Beschleunigungsvektor steht senkrecht auf dem Geschwindigkeitsvektor und zeigt zum Kreismittelpunkt.

${\displaystyle {\vec {a}}={\underset {\Delta t\rightarrow 0}{\lim }}{\frac {\Delta {\vec {v}}}{\Delta t}}\Rightarrow {\vec {v}}\perp {\vec {a}}}$

Die Richtung der Beschleunigung ist damit geklärt nicht jedoch der Betrag. Hierbei hilft die Kleinwinkelnäherung, bei der die Bogenlänge zwischen den gleich langen Geschwindigkeitsvektoren zunehmend dem direkten Abstand zwischen den Vektorspitzen entspricht. Da sich die Winkeländerung der Kreisbewegung auch in den Geschwindigkeitsvektoren widerspiegelt, kann folgende Gleichsetzung der Grenzübergänge erfolgen:

${\displaystyle |{\vec {a}}|={\underset {\Delta t\rightarrow 0}{\lim }}{\frac {|\Delta {\vec {v}}|}{\Delta t}}=v\cdot {\underset {\Delta t\rightarrow 0}{\lim }}{\frac {\Delta {\varphi }}{\Delta t}}=v\cdot \omega =R\cdot \omega ^{2}={\frac {v^{2}}{R}}}$.

Da der Beschleunigungsvektor immer Richtung Kreismittelpunkt zeigt trägt er die Bezeichnung Zentripetalbeschleunigung und in Verbindung mit der Masse gilt gleiches für die Zentripetalkraft.

Geschwindigkeit

Die Geschwindigkeit ist die Ableitung des Ortes. Dabei muss in Polarkoordinaten der Ortsvektor mitdifferenziert werden. Da der Abstand konstant ist, folgt

${\displaystyle {\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}(R{\vec {e}}_{r})=R{\frac {{\vec {e}}_{r}}{\mathrm {d} t}}}$.

Die Ableitung des Einheitsvektor in ${\displaystyle r}$-Richtung ist proportional zu dem Einheitsvektor in ${\displaystyle \varphi }$-Richtung, da

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\begin{pmatrix}R\cos \varphi \\R\sin \varphi \end{pmatrix}}={\begin{pmatrix}-R{\frac {\mathrm {d} \varphi }{\mathrm {d} t}}\sin \varphi \\R{\frac {\mathrm {d} \varphi }{\mathrm {d} t}}\cos \varphi \end{pmatrix}}}$

orthogonal zu ${\displaystyle {\vec {e}}_{r}}$ ist. Für die Geschwindigkeit gilt damit

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {r}}=R{\frac {\mathrm {d} \varphi }{\mathrm {d} t}}{\vec {e}}_{\varphi }=R\omega {\vec {e}}_{\varphi }}$

mit der Winkelgeschwindigkeit ${\displaystyle \omega ={\frac {\mathrm {d} \varphi }{\mathrm {d} t}}}$.

Beschleunigung

Im Fall der Bewegungen ist der Betrag der Geschwindigkeit konstant. Wie im Fall der Geschwindigkeit reduziert sich die zeitliche Ableitung auf die Ableitung des Richtungsvektors. Die Beschleunigung der gleichförmigen Kreisbewegung lässt sich daher mittels

${\displaystyle {\vec {a}}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}{\vec {v}}(t)={\frac {\mathrm {d} }{\mathrm {d} t}}\left(R\omega {\vec {e}}_{\varphi }(t)\right)=R\omega {\frac {\mathrm {d} {\vec {e}}_{\varphi }}{\mathrm {d} t}}}$

berechnen. Mit

${\displaystyle {\frac {\mathrm {d} {\vec {e}}_{\varphi }}{\mathrm {d} t}}=-{\frac {\mathrm {d} \varphi }{\mathrm {d} t}}{\vec {e}}_{r}(t)=-\omega {\vec {e}}_{r}(t)\ ,}$

folgt

${\displaystyle {\vec {a}}(t)=R\left(\omega {\frac {\mathrm {d} {\vec {e}}_{\varphi }}{\mathrm {d} t}}\right)=-R\omega ^{2}{\vec {e}}_{r}(t)}$.