Ergodische Lakunarität - die „Vernummerung“ der Welt#

„Aus der Nähe betrachtet, sehe man hinter jedem Ereignis die unendliche Feinheit des Kausalgewebes. Trete man weit genug zurück, offenbarten sich die großen Muster. Freiheit und Zufall seien eine Frage der mittleren Entfernung, eine Sache des Abstands.“
Kehlmann, Daniel. „Die Vermessung der Welt“ (2005)

„Nun wollte man sich ein Maß für Ordnung oder negative Entropie wünschen, zweifellos verwandt mit Information oder doch Instruktion. Das ist aber noch nicht gelungen, zumal die Physiker, die gewohnt sind, Entropie nur quantitativ zu fassen, Schrödinger nicht gefolgt sind.“
Riedl, Rupert, „Strukturen der Komplexität“ (2000)

Was ist eine Nummer? Wir alle denken, das sei doch klar: eine Nummer ist eine Zahl die etwas bezeichnet. Eine Autonummer kennzeichnet unser Auto, so dass es eine unverwechselbare Identität wird und sich aus der Masse der anderen Autos gleicher Type leicht heraushebt. Oder eine Kontonummer bei der Bank: sie sagt, wem das Konto gehört und wie viel drauf liegt. Eine Hausnummer stellt klar, welches der vielen Häuser in einer Straße gemeint ist. Mathematisch gesprochen ist eine Nummer eine Zahl in der Verwendung als Cantor-Ordinal. Georg Cantor (1845-1918) war ein berühmter Mathematiker, der sich mit der Abzählbarkeit von Elementen einer Menge befasst hat.

Halten wir fest: eine Nummer ist eine Zahl, die in einer besonderen Art verwendet wird. Aber was ist, wenn wir Zahlen zur Angabe von Messwerten verwenden? Beispielsweise zur Mitteilung, welche Temperatur gerade gemessen wurde? Hier ist die Zahl in einer ganz anderen Verwendung. Sie ist nun eine Größenangabe, eine Quantität. Quantitative Zahlen begleiten uns durch das ganze Leben. Ganze Beamtenheere sind damit beschäftigt, Zahlen über die Bürger eines Staates zu sammeln, zu ordnen, mit Nummern zu verknüpfen und so möglichst viel über uns Bürger zu wissen. Erst die Verbindung zwischen Zahl und Nummer ermöglicht diesen Wissenszuwachs. Wir sind so daran gewöhnt, dass wir das gar nicht mehr bewusst wahrnehmen. Mit Beginn dieses Jahrhunderts ist eine historisch völlig neue Situation eingetreten. Nummern und Zahlen werden in gigantischen Computer-Netzwerken gesammelt und somit verarbeitbar gemacht. Jede Sekunde kommen Milliarden an Zahlen und Nummern dazu. Die „Ver-Nummerung“ der Welt nimmt immer mehr an Fahrt auf.

Die Verwendung der Zahlen als Quantitäts-Maß oder Identitätsmerkmal ist jedoch noch nicht die ganze Möglichkeit der Zahlenverwendung. Es gibt noch zwei wesentlich exotischere Verwendungsmöglichkeiten. Die Zahl als Gödel-Nummer und die Zahl als Morphem.

Der Mathematiker Kurt Gödel (1906-1978) hat in der ersten Hälfte des 20-ten Jahrhunderts bewiesen, dass Algorithmen ebenfalls als Zahlen dargestellt werden können. Gödels Unvollständigkeits-Theorem besagt, dass mathematische Schlußketten in einem widerspruchsfreien Axiomensystem nicht vollständig sind. Gregory Chaitin (geb. 1947) zieht daraus den logischen Schluß, das Mathematik in sich Kreativität trägt und somit evolutionär ist. Damit steht er im Gegensatz zu David Hilbert (1862-1943), der die Mathematik noch als in sich geschlossenes System betrachtete, das man grundsätzlich vollständig verstehen könnte, wenn man von einer endlichen Anzahl von Axiomen ausgeht. Damals haben sich die meisten Mathematiker dieser Meinung angeschlossen.

Alan Turing (1912-1954) hat mit seiner „Universellen-Turing-Maschine“ gezeigt, dass man mit einem Computer alle denkmöglichen mathematischen Zusammenhänge errechnen kann. Die einzige Begrenzung ist dabei die verfügbare Zeit und die Geschwindigkeit der verwendeten Rechenmaschinen (Computer). Man spricht in diesem Zusammenhang auch von der „Nach-Gödel-Mathematik“ oder der konkreten Mathematik. Dies ist auch das Forschungsgebiet des IHI (Institut für Humaninformatik).

Das IHI geht von der Annahme aus, man könne alle Zahlen, die je von Menschen und Maschinen erzeugt wurden, in einem riesigen Speicher hintereinander in einer gigantischen Monsterzahl aufschreiben und damit computabel machen. Dabei spielt es keine Rolle, ob nur eine Turing-Maschine oder sehr viele gleichzeitig beteiligt sind. Auch, ob die Rechner biologisch oder künstlich sind, bleibt bei diesem Gedankenexperiment außer Beachtung. Hauptsache, die Rechner arbeiten weitestgehend fehlerfrei.

Was hier in dem Gedankenexperiment angenommen wurde, ist derzeit schon im Ansatz vorhanden. Man spricht dabei von der „Internet-Cloud“ oder der Cloud. Die Cloud ist die Summe aller im Internet vernetzten Computer, egal ob sie Großrechner sind oder Handys oder Mikroprozessoren in technischen Geräten wie Produktionsmaschinen, Haushaltsgeräten, Sensoren oder Menschen die mit diesen Geräten interagieren. Wir sprechen dann von symbiotischen Mensch-Maschine-Systemen.

Nun könnte man sagen, der gesamte Input in die Cloud erzeugt einen bestimmten Zahlenvorrat. In den Medien wird dafür gerne der Ausdruck Big-Data verwendet, um auf die Größe dieses Zahlenvorrates zu verweisen. Leider ist unsere derzeitige Kultur und Bildung überhaupt nicht auf dieses Phänomen vorbereitet. Nur ganz wenige Profis sind auf den Umgang mit sehr langen natürlichen Zahlen trainiert. Wir sind im Alltag gewohnt, längere Zahlen sofort abzukürzen und den größten Teil der Zahl einfach zu ignorieren. Das kann man schon daran ersehen, dass wir in der Umgangssprache für mehr als neunstellige Dezimalzahlen meist gar keine Wörter kennen, um diese Zahlen zu benennen. Oder kann jemand die Zahl

1405006117752879898543142606244511569936384000000000

noch beim Namen nennen? Obwohl sie eine ganz einmalige unverwechselbare Individualität ist. Im Computer kann man solche Zahlenmonster aber sehr leicht verarbeiten. Wir wissen auch nicht, ob diese Zahl nun eine Nummer (Ordinal) oder eine Quantität ist. Schon gar nicht können wir erkennen, ob es sich hier nicht vielleicht um ein Software-Programm oder ein Musikstück oder gar ein Gemälde handelt. In dem gegenständlichen Fall handelt es sich einfach um eine Kette von Ziffern. Datenschrott? Die Cloud ist ja voll von Datenschrott. Man schätzt, dass mehr als die Hälfte aller in der Cloud gespeicherten Daten Schrott sind. Trotzdem hindert das niemand, in diesem Schrotthaufen nach sinnvollen Strukturen zu suchen und auch zu finden. Auch wir wollen das tun.

Im Computer sieht diese Zahl ganz anders aus: 10011011111111001010110011110101110111110100 .... sie ist in der Binär-Version wesentlich länger und daher nur sehr abgekürzt dargestellt. (Für Spezialisten: es sind die ersten 19 Dezimalen der obigen Zahl). Wissenschaftler würden die Zahl wieder anders darstellen. Nämlich so: 1,40500611775 * 10^51. Laut Wikipedia könnte das die Anzahl der Protonen der gesamten Erde sein. Wer weiß? Als Nummer verwendet, wäre das dann die „Autonummer“ eines ganz bestimmten Protons im Planeten Erde einschließlich allem, was darauf „kreucht und fleucht“.

Wir haben in unserem Experiment nun zwei Verwendungen eines bestimmten Zahlenvorrates kennengelernt, es gibt aber vier Möglichkeiten:

1. Die Zahl als Quantität#

2. Die Zahl als Ordinal#

Zahlen können aber noch mehr. Sie sind auch noch ein Symbolvorrat. Je nach Zahlensystem hat jede Zahl einen begrenzten Vorrat an Ziffernsymbolen. Zwei dieser Zahlensysteme haben wir oben schon verwendet: das Dezimalsystem und das Binärsystem. Ersteres ist uns das geläufigste, es umfasst die Ziffern 0 bis 9. Das binäre System hat nur zwei Symbole 0 und 1. Die Römischen Zahlen arbeiten mit 7 Symbolen. Das Bitcoin-System verwendet gar 58 Symbole für seine Zugangsschlüssel.

Nun ist es an der Zeit, die obige Frage zu beantworten, was dieses lange Zahlenungetüm für eine geheime Botschaft in sich birgt. Es ist keine zufällige Aneinanderreihung von beliebigen Ziffern, sondern das Ergebnis eines ganz bestimmten Algorithmus, der auf die Zahl 42 angewendet wurde. Man nennt diesen Algorithmus die Faktorielle einer Zahl.

Die Zahl 42 ist ein Zitat aus dem mehrfach verfilmten Roman "Per Anhalter durch die Galaxis" des englischen Autors Douglas Adams (1952-2001). In diesem Roman ist die von einem Supercomputer nach einigen Millionen Jahren Rechenzeit gegebene Antwort auf die Frage „nach dem Leben, dem Universum und dem ganzen Rest“ (englisch “life, the universe and everything”): "42".

Die Zahl 42 hat aber noch eine andere bemerkenswerte Eigenschaft. Sie ist das Bindeglied zwischen einem Primzahlzwilling, nämlich 41 und 43. Solche Primzahl-Zwillinge kommen überall im Zahlenvorrat vor. Primzahlen spielen eine außerordentlich wichtige Rolle bei der Verschlüsselung von Botschaften im Internet und bei den Krypto-Währungen.

Binär sieht die Zahl „42“ so aus: 101010. Man kann sie aber auch so schreiben (als Morphem):

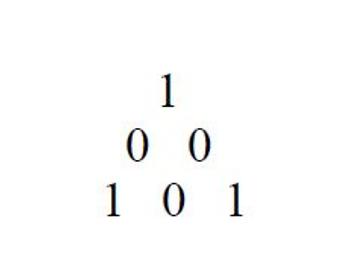
Dann haben wir das Dreieck als geometrische Grundlage aller Flächen. Die Triangulation ist das Standard-Werkzeug für die moderne Finite-Elemente Konstruktionsmethode, die nicht mehr aus der Architektur und der Industrie wegzudenken ist.

„Die Fakultät (manchmal, besonders in Österreich, auch Faktorielle genannt) ist in der Mathematik eine Funktion, die einer natürlichen Zahl das Produkt aller natürlichen Zahlen (ohne Null) kleiner und gleich dieser Zahl zuordnet. Sie wird durch ein dem Argument nachgestelltes Ausrufezeichen („!“) abgekürzt. Diese Notation wurde erstmals 1808 von dem elsässischen Mathematiker Christian Kramp (1760–1826) verwendet, der um 1798 auch die Bezeichnung faculté „Fähigkeit“ dafür einführte“ sagt Wikipedia dazu.

Diese Funktion wird hauptsächlich in der Kombinatorik verwendet, wo untersucht wird, wie viele Möglichkeiten der Anordnung einer Menge gegebener Elemente vorhanden sind, um eine Ereigniswahrscheinlichkeit zu errechnen. Zum Beispiel beim Lotto oder in der Gas-Physik. Darauf kommen wir später noch zurück.

Hier der in unserem Beispiel verwendete Faktorisierungs-Algorithmus

Das Ergebnis ist unser oben vorgestelltes „Zahlenmonster“.

Wenn wir uns den Algorithmus ansehen, können wir feststellen, dass auch er aus Symbolen besteht. Allerdings nicht nur aus Ziffern sondern auch aus Buchstaben und Sonderzeichen. Sie werden in der Software-Branche als ASCII-Zeichen bezeichnet und sind genormt.

Mathematisch wird diese Verwendung „Gödel-Nummern“ genannt, aber auch performative Zeichen, weil sie Anordnungs- oder Befehlscharakter haben und den Rechner zu einer bestimmten Handlung veranlassen. Jede Software besteht aus einer Mischung von solchen performativen Zeichen und Quantitätszahlen sowie Ordinalen. Zusammen ergeben sie eine lange Reihe binärer Ziffern, die ihrerseits den Zahlenvorrat der Cloud bilden. Wir sprechen da von immensen Zahlenvorräten! Nun kommen wir schließlich zum letzten Verwendungszweck von Zahlenvorräten, die den meisten Menschen am wenigsten bewusst sind, obwohl sie täglich damit zu tun haben. Wir sprechen von der Zahl als Morphem. Ein Morphem ist ein gestaltbildendes Element. Die Fotos in unserem Handy sind Morpheme.

Das Konzept der Morphologie stammt aus der Denkwelt der Biologen, die die Morphologie dazu benutzen, die ungeheure Formenvielfalt in der Natur zur Klassenbildung und Einteilung von Gattungen zu verwenden. Der Biologe und Erkenntnisforscher Rupert Riedl (1925-2005), der eng mit dem IHI verbunden war, hat in seinem Hauptwerk „Die Strukturen der Komplexität“ (2000) Grundlegendes herausgearbeitet und vieles, was später Gregory Chaitin in seiner Theorie der Metabiologie postulierte (2012), bereits zwölf Jahre früher vorweg genommen. Allerdings hat Riedl in Fragen der Komplexitätsmessung nur bei den Physikern nachgefragt und leider nicht bei den Mathematikern. Darum kam er zu dem für ihn unbefriedigenden Befund: „Nun wollte man sich ein Maß für Ordnung oder negative Entropie wünschen, zweifellos verwandt mit Information oder doch Instruktion (Riedl 1975). Das ist aber noch nicht gelungen, zumal die Physiker, die gewohnt sind, Entropie nur quantitativ zu fassen, Schrödinger nicht gefolgt sind.“

Er bezieht sich hier auf den Physiker und Nobelpreisträger Erwin Schrödinger (1887- 1961), der nicht nur die Quantenphysik mitbegründet hat, sondern auch in seinem Buch „Was ist Leben“ (1944) wesentliche Anregungen für die Entdeckung der DNA geliefert hat. Den Entropie-Begriff hat Riedl von Ludwig Boltzmann (1844-1906) übernommen. Boltzmann hat auch das erster das Phänomen der Ergodizität bei Gasen beschrieben.

Fassen wir die vier Verwendungsmöglichkeiten von Zahlen zusammen:

1. Zahl als Quantität (Messen, Zählen)#

2. Zahl als Cantor-Ordinal (Nummer, Identifikation)#

3. Zahl als Gödel-Nummer (performative Zeichen, Algorithmen, Software)#

4. Zahl als IHI-Morphem (geometrische Figuren, Bilder, Musik, Sprache)#

1 & 2 ist die Domäne der Empirie und der Naturwissenschaften 3 & 4 ist die Domäne der Geisteswissenschaften alle 4 sind die Domäne der konkreten Mathematik und der IT.

Hier ist nun nachstehend eine andere 400-stellige Binärzahl als Matrize dargestellt. Zur besseren Wahrnehmung des Muster-Charakters sind die 0-Stellen rot gefärbt. Sie sind gewissermaßen die „freien Parkplätze“ in der Matrix. Die Lücken, die Lakunaritäten. Wir Menschen sind gewohnt, die Dinge zu sehen und nicht die Zwischenräume. Wir sind im Normalfall ein wenig Lakunaritäts-blind.

In dieser Zahl ist die Lakunarität ziemlich genau 50%. Anders ausgedrückt, die Wahrscheinlichkeit, eine Leerstelle in der Matrix zu treffen, beträgt 0,5. Die rechte Seite zeigt die Struktur der Matrix mit geglätteten Umrisslinien, es handelt sich um eine geschlossene Jordankurve, die das ästhetisch Bildhafte dieser Matrix klarer erkennbar macht. Eine Jordankurve hat die Eigenschaft, die Fläche in ein eindeutiges „Innen“ und ein „Außen“ zu trennen. Philosophischer ausgedrückt, trennt die Jordankurve das Sein vom Nichtsein.

Die Jordankurve als Morphem ist ein wichtiger Forschungsgegenstand des IHI, weil sie die geometrische „Haut“ von Agglomerationen bildet. Sie trennt Datenpunkte in zugehörige und nicht zugehörige. Wie die Haut unser Innen von der Außenwelt abgrenzt, so kann die Jordankurve Mengen zusammengehöriger Elemente umgrenzen und so von der Umwelt unterscheidbar machen. Das wird betriebswirtschaftlich mit der Technik der Venn- Diagramme am IHI angewendet, wie im 72. IHI-Bericht beschrieben. Das Verfahren wird in der Daten-Cloud als Clustering bezeichnet und dient zur Identifikation von Personen oder Sachen anhand zufällig gesammelter Informationen. Einer der großen Hoffnungsmärkte der Zukunft und schon jetzt Quelle von Milliardengewinnen (Google, Amazon). Die Jordankurve ist nach dem Mathematiker Camille Jordan (1838-1922) benannt, der die wichtigsten Eigenschaften dieses geometrischen Objektes definiert hat.

Die wesentlichsten Eigenschaften einer Jordankurve sind die eindeutige Trennung zwischen Innen und Außen, die Selbstmeidung (die Kurve darf sich nicht berühren oder gar schneiden), die Möglichkeit aus Geraden zusammengestellt zu werden (Digitalisierung) und die Gesamtkrümmung von 2π. Diese und weitere Eigenschaften machen die Jordankurve zu einem interessanten Forschungsgegenstand der Humaninformatik.

Immerhin hat die Evolution schon sehr früh die Jordankurven als Umrisslinien zur Entwicklung des Auges und des Sehvermögens verwendet.

Matrix mit 20×20 Symbolen {1,0} ergibt als Zahl 2^400 = 2,58*10^120

Als wäre es nicht schon wichtig genug, die Jordankurve als „Haut“ einer mathematischen Menge zu sehen, hat sie auch noch eine weitere bemerkenswerte Eigenschaft:

Zu jedem Punkt innerhalb einer selbstmeidenden Jordankurve gibt es einen Kreis, der mindestens einen Punkt der Kurve berührt, den Inkreis, und einen Kreis mit gleichem Mittelpunkt, der mindestens einen Punkt der Kurve von außen berührt, den Umkreis. Zwischen den beiden konzentrischen Kreisen befinden sich dann alle Punkte der Jordankurve. Auf diese Weise bekommt die Kurve ein eindeutiges Maximum und ein Minimum als Begrenzung, die man als Grenzen eines Zustandsraumes auffassen kann. Eine andere Möglichkeit ist, ein Quadrat zu finden, dessen vier Eckpunkte genau auf der Jordankurve liegen. Die Toeplitz-Vermutung besagt, dass dies für wirklich jede Jordankurve gilt, wurde aber noch nicht im strengen Sinne bewiesen. Für praktische Zwecke wird die Toeplitz-Quadrierung bei BEKO im Bereich der Pano-Tours zur Gebäudedigitalisierung eingesetzt (71. IHI-Bericht).

Ein Zustandsraum ist ein abstrakter, mindestens zweidimensionaler Raum, in dem jeder Punkt ein „Ereignis“ darstellt. Diese Vorstellung hat sich Ludwig Boltzmann zu Nutze gemacht, um ein Modell des Verhaltens von Gasen zu untersuchen. Er hat dabei festgestellt, dass Gase jeden Zustandsraum nach einer gewissen Zeit vollständig und gleichmäßig ausfüllen. Die Moleküle des Gases stoßen chaotisch aneinander und taumeln dadurch in einer Brown'schen Bewegung im Raum umher. Heute in der Informatik spricht man eher vom Random-Walk und bemüht gerne das Bild von einem Zecher, der betrunken durch die Gegend taumelt.

Boltzmann dachte, dass das taumelnde Objekt irgendwann jeden Punkt im Raum mindestens einmal erreicht und nennt diesen Zustand ergodisch. Ein ergodischer Zustandsraum hat daher keine Lücken, also die ergodische Lakunarität von 0. Wie eine ständig vollgeparkte Tiefgarage. Das gilt allerdings nur für eine statische Betrachtungsweise. In der Dynamik gibt es immer zeitlich begrenzte Lücken. Man spricht dann von einer Geometrodynamik eines Zustandsraumes. Einstein gründete auf dieser Vorstellung seine Allgemeine Relativitätstheorie.

Wenn wir die obige lange Zahl des Ergebnisses aus der Faktorisierung der Zahl 42 in einen gedachten zweidimensionalen Zustandsraum einzeichnen, entsteht diese Figur:

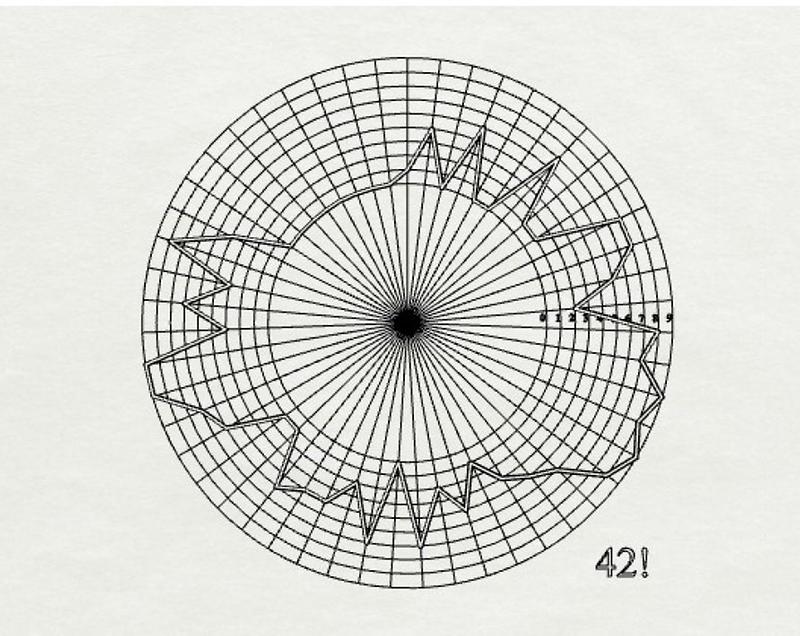
Die ringförmige Fläche wird durch die Anzahl der Dezimalstellen definiert und die Ringbreite spannt den Raum des Symbolvorrats auf. Die dicke Jordan-Kurven-Linie verbindet die einzelnen Ziffern der Langzahl. Jede dezimale 51-stellige Zahl kann in dieser Ringfläche eingezeichnet werden. Alle Zahlen n von 0000... bis 9999... eingezeichnet würden die Ringfläche komplett schwärzen. Damit wäre die ergodische Lakunarität = 0.

Wenn nur eine Kurve, wie oben dargestellt, eingezeichnet wird, dann ist die Lakunarität = 1-1/n, also sehr hoch. Die Wahrscheinlichkeit, durch reines Probieren diese Kurve exakt zu erraten, wäre daher 1/n. Allerdings nur, wenn keine Kurve in dem stochastischen Prozess des Ausprobierens mehrfach vorkommt. In der theoretischen Informatik und der konkreten Mathematik spricht man von einem Exhaustive-Random-Search-Prozess. Der kann sehr lange dauern, wenn der ergodische Raum eine gewisse Anzahl von „Zellen“ überschreitet.

Der ungarische Mathematiker Tibor Radó (1995-1965) hat eine nicht berechenbare Funktion gefunden, die nach ihm benannt ist und die unter Programmierern unter dem Namen „Busy Beaver“ bekannt ist. Dieser gedachte fleissige Biber läuft als eine selbstgesteuerte „Turing-Maschine“ durch die Fläche und zieht eine Spur umgenagter Bäume (Ereignisse) hinter sich, bis er irgendwann ganz von alleine stehen bleibt. Schließt man diese Biber-Bahn zu einer geschlossenen Kurve, dann hat der Biber seine Arbeit getan. Man nennt das eine geschlossene Programmschleife ohne „Orakel“ also ohne eine Angabe äußerer Information zur Definition des Anhaltepunktes. Wie in obiger Abbildung gezeigt, ist das Ergebnis der Biber-Tour eine eine Zahl n. Auch die Schritte, die der Biber auf seinem Weg zurücklegen musste, werden gezählt und ergeben eine Zahl Σ(k). Es gibt einen Zusammenhang zwischen n und Σ(k). Der Mathematiker Chaitin hat herausgefunden, dass diese Radó-Funktion nicht nur für ein Maß für die Komplexität einer Zahl steht, sondern auch als mathematische Erklärung für die Selbststeuerung der Evolution dienen könnte. Auf diese Weise könnte das von Riedl so gewünschte Maß für die Ordnung der Natur vorhanden sein. Ob die Biologen diesen Impuls aus der konkreten Mathematik aufnehmen und weiterentwickeln werden, wird die Zukunft weisen.

Zahlen in Jordankurven zu verwandeln und diese dann anschließend in Töne, Farben oder andere wahrnehmbare Reize für den Menschen zu transformieren ist Gegenstand der IHI- Forschung. Dabei haben sich Kunstformate wie lyrische Texte, Musik oder Gemälde bewährt und im weiteren zu verwertbaren Produkten geführt. Die kreativen Experimente führen auch auf die Spur, wie die Natur in der Evolution ihre überall beobachtbare Kreativität entfalten konnte.