Interpolation (Mathematik)
In der numerischen Mathematik bezeichnet der Begriff Interpolation (aus lateinisch inter = dazwischen und polire = glätten, schleifen) eine Klasse von Problemen und Verfahren. Zu gegebenen diskreten Daten (z. B. Messwerten) soll eine stetige Funktion (die sogenannte Interpolante oder Interpolierende) gefunden werden, die diese Daten abbildet. Man sagt dann, die Funktion interpoliert die Daten.

Einführung
Manchmal sind von einer Funktion nur einzelne Punkte bekannt, aber keine analytische Beschreibung der Funktion, durch die sie an beliebigen Stellen ausgewertet werden könnte. Ein Beispiel sind Punkte als Resultat einer physikalischen Messung. Könnte man die Punkte durch eine (eventuell glatte) Kurve verbinden, so wäre es möglich, die unbekannte Funktion an den dazwischenliegenden Stellen zu schätzen. In anderen Fällen soll eine schwierig handhabbare Funktion näherungsweise durch eine einfachere dargestellt werden. Eine Interpolationsfunktion kann diese Anforderung der Einfachheit erfüllen. Diese Aufgabe bezeichnet man als Interpolationsproblem. Es gibt für das Problem mehrere Lösungen, der Anwender muss zunächst geeignete Ansatzfunktionen wählen. Je nach Ansatzfunktionen erhalten wir eine andere Interpolante.
Die Interpolation ist eine Art der Approximation: Die betrachtete Funktion wird durch die Interpolationsfunktion in den Stützstellen exakt wiedergegeben und in den restlichen Punkten immerhin näherungsweise. Die Approximationsgüte hängt vom Ansatz ab. Um sie zu schätzen, werden Zusatzinformationen über die Funktion benötigt. Diese ergeben sich auch bei Unkenntnis von meist in natürlicher Weise: Beschränktheit, Stetigkeit oder Differenzierbarkeit lassen sich häufig voraussetzen.
Bei anderen Approximationsverfahren wie der Ausgleichungsrechnung wird nicht gefordert, dass die Messdaten exakt wiedergegeben werden. Dadurch unterscheiden sich diese Verfahren von der Interpolation. Bei dem verwandten Problem der Extrapolation werden Werte geschätzt, die über den Definitionsbereich der Daten hinausgehen.
Interpolationsprobleme
Das allgemeine Interpolationsproblem
Gegeben seien Paare reeller oder komplexer Zahlen als Stützpunkte. Man wählt eine Ansatzfunktion , die sowohl von als auch von weiteren Parametern abhängt. Als Interpolationsproblem bezeichnet man die Aufgabe, die so zu wählen, dass ist.
Das lineare Interpolationsproblem
Man spricht von einem linearen Interpolationsproblem, wenn nur linear von den abhängt, d. h.
- .
Insbesondere die Polynominterpolation ist ein solches lineares Interpolationsproblem. Für die Polynominterpolation gilt
- .
Spezialfälle für , und nennt man lineare, quadratische und kubische Interpolation. In zwei Dimensionen spricht man entsprechend von bilinear, biquadratisch und bikubisch.
Des Weiteren ist die trigonometrische Interpolation eine lineare Interpolation:
Nichtlineare Interpolationsprobleme
Zu den wichtigsten nichtlinearen Interpolationsproblemen zählt
- das rationale:
Interpolationsverfahren
Abschnittsweise konstante Interpolation
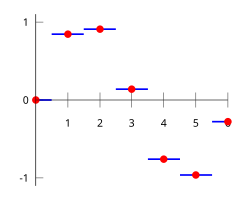
Als einfache Interpolationsmethode kann der nächstgelegenen Datenwert gesucht werden und dem aktuellen Punkt dessen Wert zugewiesen werden.[1] Bei einfachen Problemen ist es unwahrscheinlich, dass diese Methode verwendet wird, da die lineare Interpolation fast genauso einfach ist. Bei höherdimensionalen multivariaten Interpolationen könnte diese Methode aufgrund ihrer Schnelligkeit und Einfachheit dennoch eine gute Wahl sein.
Lineare Interpolation
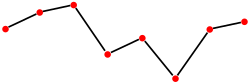
Die von Isaac Newton begründete lineare Interpolation ist am einfachsten und wird wohl in der Praxis am häufigsten benutzt. Hier werden zwei gegebene Datenpunkte () und () durch eine Strecke verbunden. Es gilt:
Dies entspricht einer Konvexkombination der Endpunkte und .
Detaillierte Erläuterungen siehe Allgemeine lineare Interpolation.
Höhergradige Polynome
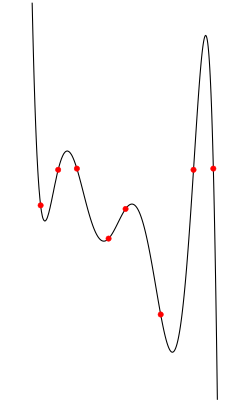
Zu paarweise verschiedenen Datenpunkten gibt es genau ein Interpolationspolynom -ten Grades, das an den vorgegebenen Stützstellen mit den vorgegebenen Stützwerten übereinstimmt. Die Bestimmung der Koeffizienten erfordert die Lösung eines linearen Gleichungssystems. Die Existenz eines solchen Interpolationspolynoms sieht man z. B. mit Hilfe der Formel von Lagrange
- .
Diese Funktion nimmt an den Stellen die Werte an. Die Eindeutigkeit folgt aus der bekannten Tatsache, dass ein Polynom -ten Grades höchstens Nullstellen besitzt.
Weitere Verfahren zur Polynominterpolation siehe dort.
Stückweise Interpolation
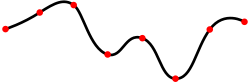
Da Polynome mit zunehmendem Grad immer instabiler werden, d. h. stark zwischen den Interpolationspunkten schwingen, werden in der Praxis Polynome mit einem Grad größer als 5 kaum eingesetzt. Stattdessen interpoliert man einen großen Datensatz stückweise. Im Fall der linearen Interpolation wäre das ein Polygonzug oder linearer Spline, bei stückweisen Polynomen höheren Grades spricht man auch von Spline-Interpolation. Bei abschnittsweise definierten Interpolanten ist die Frage der Stetigkeit und Differenzierbarkeit an den Stützstellen von großer Bedeutung.
Im mehrdimensionalen Fall basiert insbesondere die Methode der finiten Elemente für elliptische Probleme zweiter Ordnung auf dem Einsatz stetiger Splines, oft auf Dreiecksgittern. Fehlerabschätzungen für die Finite-Element-Methode basieren auf entsprechenden Abschätzungen des Interpolationsfehlers.
Hermiteinterpolation
Sind zusätzlich zu den Stützstellen auch noch die -Ableitungen zu interpolieren, so spricht man von einem Hermite-Interpolationsproblem. Die Lösung dieses Problems lässt sich analog zum Lagrange-Verfahren ebenfalls in geschlossener Form angeben.
Im mehrdimensionalen Fall basiert insbesondere die Methode der finiten Elemente für elliptische Probleme vierter Ordnung auf dem Einsatz stetig differenzierbarer Splines. Auf Dreiecksgittern ist deren Konstruktion nicht so einfach.
Trigonometrische Interpolation
Wählt man als Ansatzfunktion ein trigonometrisches Polynom, so erhält man eine trigonometrische Interpolation. Die Interpolationsformel
entspricht einer Fourier-Entwicklung der unbekannten Interpolanten. Die Fourier-Koeffizienten und berechnen sich zu
- und .
Dabei wird angenommen, dass die Stützstellen im Intervall äquidistant verteilt sowie außerhalb dieses Intervalls periodisch sind. Die Koeffizienten können effizient mit Hilfe der schnellen Fourier-Transformation berechnet werden.
Logarithmische Interpolation
Vermutet bzw. weiß man, dass den Daten eine logarithmische Funktion zugrunde liegt, so empfiehlt sich dieses Verfahren.
Bei der logarithmischen Interpolation werden zwei bekannte Datenpunkte und durch eine logarithmische Kurve verbunden. Es gilt:
Oder anders formuliert:
Beispiel: χ²-Test
Gaußprozess-Regression (Kriging)
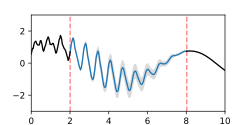
Ein sehr vielseitiges und universelles Interpolationsverfahren ist die Gaußprozess-Regression bzw. das Kriging-Verfahren. Damit können sowohl Interpolationen als auch Glättungen in beliebigen Dimensionen und auf unregelmäßigen Stützstellen durchgeführt werden. Mithilfe einer sogenannten Kovarianzfunktion können spezielle Eigenschaften der Daten beschrieben werden (z. B. die Korrelationslänge oder eine Periodizität), um damit die für das Problem optimale Interpolation durchzuführen.
Eigenschaften der Interpolationsmethode:
- Geeignet für unregelmäßige Stützstellen
- Interpolation in beliebigen Dimensionen (z. B. Flächen-Interpolation)
- Optimale Interpolation von glatten, periodischen oder verrauschten Kurven
- Vorhersage des Vertrauensintervalls der Interpolation
Allgemeine lineare Interpolation
Es sei eine reelle oder komplexe stetig differenzierbare Funktion mit Nullstellenmenge , wobei alle Nullstellen einfach sein müssen. Dabei kann die Indexmenge eine endliche Menge, wie z. B. , oder eine abzählbare Menge, wie oder , sein. Damit sind die Interpolationskerne gegeben als
und stetig mit dem Wert 1 an der Stelle fortgesetzt. Die Hilfsfunktion ist außerhalb der Diagonalen definiert als
- und stetig fortgesetzt zu .
Auf den Nullstellen gilt , wobei das Kronecker-Delta verwendet wurde.
Sind jetzt Werte für jedes vorgegeben, so ist eine Interpolationsfunktion definiert durch
- .
Im Falle einer abzählbaren Nullstellenmenge muss die Konvergenzbedingung
erfüllt sein.
Beispiele
- Mit vorgegebenen Stützstellen und einer reellen Funktion mit , kann die Funktion gebildet werden. Dann erhält man
-
- .
- Das aus resultierende Interpolationsverfahren ist die Lagrange-Interpolation. Andere Beispiele sind für nach Unendlich gegen Null fallende Interpolationsfunktionen oder für eine beschränkte Interpolationsfunktion mit übersichtlicher Berechnungsformel.
- Mit dem Kreisteilungspolynom , d. h. den -ten Einheitswurzeln , , als Stützstellen, ergibt sich die Diskrete Fourier-Transformation als Verfahren zur Berechnung der Koeffizienten des Interpolationspolynoms. Es gilt und allgemein , so dass
-
- ist.
- Mit und den Nullstellen , , ergibt sich als Interpolationsfunktion die Kardinalreihe
- .
Diese spielt eine zentrale Rolle im Nyquist-Shannon-Abtasttheorem. Die Konvergenzbedingung lautet
- .
Stützstellendarstellung von Polynomen
Sei ein Polynom. Dieses Polynom lässt sich in der sogenannten Koeffizientendarstellung durch die Angabe des Vektors darstellen. Eine alternative Darstellung, die ohne die Koeffizienten auskommt, besteht in der Stützstellendarstellung. Dabei wird das Polynom für Werte mit und ausgewertet, d. h., es werden die Funktionswerte berechnet. Das Paar von Vektoren bezeichnet man als die Stützstellendarstellung des Polynoms . Ein wesentlicher Vorteil dieser Darstellung besteht darin, dass zwei Polynome in Stützstellendarstellung in (s. Landau-Symbole) Schritten multipliziert werden können. In Koeffizientendarstellung werden hingegen Schritte benötigt. Die Transformation von der Koeffizienten- in die Stützstellendarstellung ist daher von spezieller Bedeutung und wird als Fourier-Transformation bezeichnet. Die Rücktransformation wird durch Interpolation erreicht.
Anwendungen

Hinsichtlicher vieler Anwendungen von Interpolationsverfahren besteht die Vorstellung, dass hierbei neue Information aus bestehenden Daten hinzugewonnen wird. Dies ist aber unrichtig. Vielmehr wird durch die Interpolation ein möglicher Verlauf einer kontinuierlichen Funktion zwischen den bekannten Abtastpunkten abgeschätzt. Diese Abschätzung basiert auf der Annahme, dass der Verlauf einigermaßen „glatt“ ist, was in den vielen Fällen zu plausiblen Resultaten führt. Diese Annahme muss aber nicht notwendigerweise so zutreffen, denn die höheren Frequenzanteile, die bei der Digitalisierung eines Signals aufgrund des Abtasttheorems verloren gegangen sind, können grundsätzlich durch eine anschließende Interpolation nicht wieder rekonstruiert werden. Damit muss für jede Interpolation eine Annahme über die maximal zuvor enthaltene Frequenz gemacht werden. Nur wenn diese bekannt ist und eine ideale Digitalisierung vorlag, gelingt die Rekonstruktion perfekt. In den meisten Fällen wird damit dem Signal eine gewisse Menge an Falschinformation hinzugefügt.
Ein bekanntes Problem der Interpolation in der digitalen Signalverarbeitung ist die der Umwandlung eines Signals mit einer niedrigen Abtastrate in eine hohe (siehe Abtastratenkonvertierung). Dabei werden neue Abtastwerte für das Ausgabesignal aus denen des Eingabesignals interpoliert. Je nach Anwendungsfall werden dazu entweder Nullen eingefügt, die jeweils vorherigen Werte wiederholt oder eine von mehreren Interpolationen (linear, bilinear oder wavelet) genutzt.
Ein Spezialfall ist die Skalierung von Bildern in der Computergrafik: Da bei vielen Bildern maximale Kontraste benutzt werden, liegen Daten vor, bei denen das Nyquist-Kriterium verletzt wurde. Diese Bilder sind nur durch ganzzahlige Faktoren sinnvoll skalierbar, da sich bei unganzzahligen Ansätzen die Notwendigkeit ergibt, Pixelwerte für Zwischenkoordinaten zu berechnen, wodurch Alias-Effekte auftreten (Moiré-Muster).
Ein weiterer Anwendungsfall ist die Gewinnung von Phasen- und Amplitudeninformationen für Zwischenfrequenzen bei einer FFT: Hier sind spezielle Interpolationsformeln nötig. Diese erzeugen aber ebenfalls keine neuen Informationen, sondern machen nur die bereits enthaltenen Informationen der Stützpunkte leichter interpretierbar.[2]
Interpolation in höheren Dimensionen
Die oben gezeigten einfachen Verfahren sind meist nur für 1D-Probleme beschrieben. Für höhere Dimensionen geeignet sind Spline-Interpolationen mit z. B. Thinplate-Splines oder anderen Radial-Basisfunktionen oder das Kriging-Verfahren bzw. die Gaußprozessregression. Eine einfache Möglichkeit zur Interpolation von Punkten in höheren Dimensionen (), die in einem regelmäßigen Gitter vorliegen, ist die rekursive Anwendung von 1D-Interpolationen.
Am Beispiel der bilinearen Interpolation sei dieses erläutert.
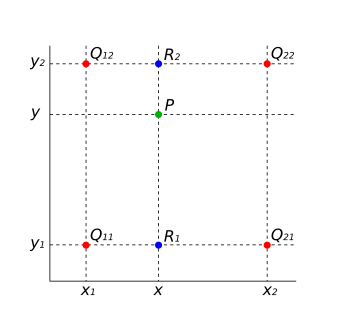 Gegeben sind Zahlenwerte an den Eckpunkten , , und . Gesucht ist der interpolierte Wert an Stelle .
Gegeben sind Zahlenwerte an den Eckpunkten , , und . Gesucht ist der interpolierte Wert an Stelle .
Vorgehensweise: Die lineare Interpolation wird zweimal angewendet, z. B. zuerst für die x-Richtung. Es wird aus und mit der linearen 1D-Interpolation ermittelt. Anschließend wird auf gleiche Weise bestimmt. Der Wert an ergibt sich als lineare 1D-Interpolation in y-Richtung zwischen und .
3D: Für eine trilineare Interpolation gibt es Eckpunkte mit Zahlenwerten. Die erste Interpolation auf der x-Achse ergibt Zwischenpunkte, die auf einer Ebene senkrecht zu liegen. In dieser Ebene wird in y-Richtung interpoliert bei und es ergeben sich Zwischenpunkte auf einer Linie in z-Richtung an Position . Die letzte Interpolation auf dieser Linie ergibt schließlich Punkte, also die gesuchte Lösung.
Für eine beliebige Dimension ist das Verfahren durch sukzessive Rekursion anwendbar.
Siehe auch
Literatur
- Josef Stoer: Numerische Mathematik 1. 8. Auflage, Springer 1999.
- Bernd Jähne: Digitale Bildverarbeitung. 4. Auflage, Springer 1997.
- Oppenheim, Schafer: Zeitdiskrete Signalverarbeitung. Oldenbourg 1992.
- Crochiere, Rabiner: Multirate Digital Signal Processing. Prentice Hall 1983.
Weblinks
- Online-Tool für Lineare und Quadratische Interpolation mit Visualisierung
- Seite zu Newton, Lagrange und Cubic Spline ebenfalls mit Java-Applet
- Räumliche Analyse (Interpolation) mit QGIS
Einzelnachweise
- ↑ U. Rüde: Rekonstruktion kontinuierlicher Daten Interpolation 1D. Friedrich-Alexander Universität Erlangen-Nürnberg, 2017, abgerufen am 6. Mai 2023.
- ↑ Z. Liu, J. Himmel, K.W. Bonfig: Improved Processing of Harmonics and Interharmonics by Time-Domain Averaging. In: IEEE Transactions on Power Delivery. Band 20, Nr. 4, Oktober 2005, ISSN 0885-8977, S. 2370–2380, doi:10.1109/TPWRD.2005.855477 (ieee.org [abgerufen am 1. Mai 2024]).
License Information of Images on page#
| Image Description | Credit | Artist | License Name | File |
|---|---|---|---|---|
| SVG version of public domain image Bilinear_interpolation.fig from en.wikipedia.org | Eigenes Werk | Bocsika | Datei:BilinearInterpolation.svg | |
| Gaussian process posterior of function with gap visualized by mean function and confidence interval | Eigenes Werk | Physikinger | Datei:Gaussianprocess gapMean.svg | |
| Stückweise lineare Interpolation | Eigenes Werk | Adrichel | Datei:Linear interpolation.svg | |
| Illustration of constant interpolation, more precisely en:Nearest neighbor interpolation on the same dataset as listed in Interpolation . | self-made in Gnuplot | Berland | Datei:Piecewise constant.svg | |
| p ( x ) = − 30.550224302876202 + 1.3405464324655687 ⋅ x + 0.33940746902954505 ⋅ x 2 + 0.006043447628845429 ⋅ x 3 − 0.00040762779516188906 ⋅ x 4 − 0.000016598804950050045 ⋅ x 5 − 2.1597800840011248 ⋅ 10 − 7 ⋅ x 6 + − 9.533599505095986 ⋅ 10 − 10 ⋅ x 7 \displaystyle \beginalignedp(x)=&-30.550224302876202+1.3405464324655687\cdot x+0.33940746902954505\cdot x^2+0.006043447628845429\cdot x^3 &-0.00040762779516188906\cdot x^4-0.000016598804950050045\cdot x^5 &-2.1597800840011248\cdot 10^-7\cdot x^6+-9.533599505095986\cdot 10^-10\cdot x^7\endaligned Punkte: (-79.66666666666667,9.333333333333329) (-69.33333333333333,19.33333333333333) (-58.333333333333336, 19.66666666666667) (-39.666666666666664,0) (-29.666666666666664,8.333333333333329) (-9,-21.33333333333333) (10.333333333333329,19.33333333333333) (22,19.66666666666667) | Eigenes Werk | MartinThoma | Datei:Polynomial-interpolation.svg | |
| Beispielpunkte zur Interpolation | Eigenes Werk | Adrichel | Datei:Punkte Interpolation.svg | |
| Spline interpolation | Eigenes Werk | Tam | Datei:Spline interpolation.svg | |
| Datei:Umbrella Nearest Neigbor.png | ||||
| Datei:Wiktfavicon en.svg |
































![{\displaystyle [0;\,2\pi ]}](/aw/img/svg/16f5f509592bc411ec6c687a6c87f8165e279556)







































































