Ein Oszillator (von lateinisch oscillare ‚schaukeln‘) ist ein schwingungsfähiges System.^[1] Dies bedeutet, dass es eine üblicherweise zeitliche Oszillation seiner Zustandsgrößen ermöglicht. Oszillation bedeutet, dass eine fortwährende Veränderung zwischen zwei Zuständen, oder um einen zentralen Punkt stattfindet, der meist der Ruhelage des Systems entspricht.^[2]

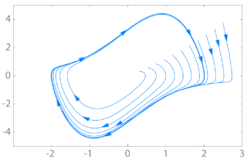
Wenn sich das Verhalten des Oszillators mit Differentialgleichungen beschreiben lässt, ist es mathematisch gesehen ein Dynamisches System. Ein solches System bezeichnet man dann als Oszillator, wenn es einen stabilen Grenzzyklus besitzt.^[3][4] Einen Zustand, bei dem ein Grenzzyklus erreicht ist, nennt man eingeschwungener Zustand. In einem solchen Zustand ist die Schwingung des Oszillators notwendigerweise periodisch.

Oszillatoren findet man überwiegend in der Elektrotechnik bzw. Elektronik und der Mechanik. Jedoch sind Systeme mit periodischem Verhalten auch aus anderen Bereichen technischen Zeitsystemen, in der Chemie, in der Biologie und in der Soziologie^[5] bekannt.

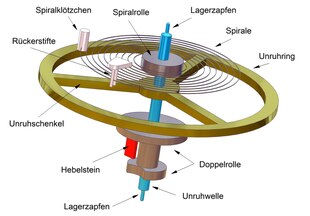
Schwingungen mechanischer oder elektrischer Systeme sind ohne zusätzliche Maßnahmen stets gedämpft. Das bedeutet, dass die Amplitude der Schwingung mit der Zeit abnimmt, wenn aktiv keine Energie von außen zugefügt wird. Ein Oszillator besitzt daher immer eine Einrichtung zur Zuführung von Energie. Dies kann beispielsweise durch mechanische Kraft, wie bei einem Uhrwerk, oder durch elektrische Spannung geschehen.

Mathematische Definition

Betrachte ein System von gewöhnlichen Differentialgleichungen

${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=f(x),\quad x\in \mathbb {R} ^{n},\quad n\geq 2}$

oder

${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=f(x,t),\quad x\in \mathbb {R} ^{n},\quad n\geq 1}$

mit einer glatten Funktion ${\displaystyle f\colon \mathbb {R} ^{n}\times \mathbb {R} \to \mathbb {R} ^{n}}$. Die Größe ${\displaystyle x}$ ist der Zustand eines physikalischen Systems. Die Menge aller Zustände wird Zustands- oder Phasenraum genannt. Die Eingangsgröße ${\displaystyle t\in \mathbb {R} }$ kann als Zeit betrachtet werden^[3] oder verallgemeinert auch aus ${\displaystyle \mathbb {R} ^{p}}$^[4] gewählt werden. Eine Lösung oder Trajektorie ${\displaystyle x_{0}(t)}$ ist periodisch, wenn eine Konstante ${\displaystyle T>0}$ existiert, sodass gilt

${\displaystyle x_{0}(t)=x_{0}(t+T)}$.

Die Konstante ${\displaystyle T}$ ist die Periode, der Kehrwert ${\displaystyle 1/T}$ die Frequenz der Schwingung. Die Menge der Zustände (bzw. des Flusses) einer solchen Lösung ist ein periodischer Orbit, auch Orbital oder Grenzzyklus genannt. Das betrachtete System heißt Oszillator, wenn für ${\displaystyle t=0}$ ein asymptotisch orbital-stabiler Orbit existiert.^[4][6] Das bedeutet, dass eine Trajektorie, die hinreichend nah an dem periodischen Orbit liegt, für alle ${\displaystyle t>0}$ auch hinreichend nah bleibt, oder präziser folgende Bedingungen erfüllt:^[6]

• Für jeden Wert ${\displaystyle \varepsilon >0}$ existiert ein ${\displaystyle \delta >0}$, sodass für ${\displaystyle |x(0)-x_{0}(0)|<\delta }$ gilt, dass ${\displaystyle |x(t)-x_{0}(t)|<\varepsilon }$ für alle ${\displaystyle t>0}$.
• Es existiert ein asymptotischer Phasenversatz ${\displaystyle \phi }$, sodass gilt ${\displaystyle \lim _{t\to \infty }\left|x(t)-x_{0}(t+\phi )\right|\to 0}$.

Oszillatoren in der Physik

Asymptotische Stabilität bedeutet attraktiv und Ljapunow-stabil. Ersteres gilt für Systeme, deren Energie sich einem Grenzwert annähert, letzteres für Systeme, deren Energie erhalten ist. Energieerhaltung bedeutet, dass bei einer Bewegung entlang eines geschlossenen Weges keine Arbeit verrichtet wird. Diese Systeme nennt man konservativ. Wie sich beispielsweise an dem Modell des dynamischen Billards sehen lässt, besitzen nicht alle konservativen Systeme einen stabilen periodischen Orbit und sind somit ein Oszillator.

Aufgrund der Energieerhaltung lässt sich das Kraftfeld eines konservativen Systems durch ein Potential beschreiben. Jedem periodischen Orbit lässt sich somit eine Energie zuordnen. Dieses Modell lässt sich für ein elektrisch geladenes Teilchen verwenden, das sich in einem elektrischen Potential bewegt. In der Quantenmechanik lassen sich mit diesem Modell z. B. Atomorbitale berechnen. Klassisch ist der Zustand ${\displaystyle x=(q,p)}$ des Oszillators durch Auslenkung ${\displaystyle q}$ des Teilchens aus der Ruhelage und seiner Geschwindigkeit bzw. seinen Impuls ${\displaystyle p}$ bestimmt.

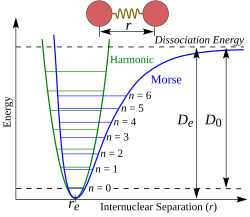
Bei genauer Betrachtung sind praktisch alle realen Oszillatoren anharmonisch. Sie lassen sich jedoch häufig näherungsweise mit dem Modell eines harmonischen Oszillators beschreiben:

${\displaystyle {\begin{aligned}{\frac {\mathrm {d} q}{\mathrm {d} t}}&=p\\{\frac {\mathrm {d} p}{\mathrm {d} t}}&=-\omega ^{2}q\\\end{aligned}}}$

Hierbei ist die Teilchenmasse entdimensionalisiert 1 gewählt, sodass

• ${\displaystyle \omega /(2\pi )}$ die Frequenz,
• ${\displaystyle \langle p^{2}\rangle =\omega ^{2}\langle q^{2}\rangle }$ die Gesamtenergie

eines Orbits ist. Die Klammern ${\displaystyle \langle \;\rangle }$ stehen für den zeitlichen Mittelwert bzw. quantenmechanischen Erwartungswert. Die Gesamtenergie folgt aus dem Äquipartitionstheorem oder Virialsatz für beliebige Oszillatoren. Quantenmechanisch sind für die Gesamtenergie nur Energieniveaus ${\displaystyle \hbar \omega (\nu +{\tfrac {1}{2}})}$ mit ${\displaystyle \nu =0,1,\dotsc }$ erlaubt. Die Konstante ${\displaystyle 2\pi \hbar }$ ist das plancksche Wirkungsquantum.

Oszillatoren in der Elektronik

Ein Oszillator in der Elektronik erzeugt ungedämpfte meist sinusförmige elektrische Schwingungen. Er arbeitet an Gleichspannung und erzeugt Wechselspannung und kann aus einem einzelnen selbstschwingenden Bauteil oder aus mehreren Bauteilen bestehen, die zu einer Oszillatorschaltung zusammengefügt werden. Diese Bauteile müssen damit eine Verstärkung > 1 haben (Ausgangsamplitude größer als Eingangsamplitude) und verstärken die Amplitude des Schwingungssignals, bis eine physikalische Begrenzung eintritt. Dies führt letztendlich zu einem stabilen Ausgangssignal.

Anforderungen an Oszillatoren sind Konstanz des Ausgangssignals in Frequenz und Amplitude und eine geringe Temperaturabhängigkeit. Manche Oszillatoren dienen der Erzeugung von Wechselspannung oder der Spannungswandlung mit hohem Wirkungsgrad (zum Beispiel Magnetron, Royer-Oszillator).

Ein Oszillator enthält immer frequenzbestimmende Bauteile, eine Begrenzung der Amplitude und einen negativen differenziellen Widerstand. Dieser wird entweder durch einen rückgekoppelten Verstärker oder durch ein Bauelement mit negativem differenziellen Widerstand wie beispielsweise eine Tunneldiode oder Lambda-Diode realisiert.

Die Amplitudenbegrenzung geschieht durch passive oder aktive Maßnahmen. Es kann eine Amplitudenregelung geben (typisch z. B. bei RC-Oszillatoren), meist wird jedoch die Eigenschaft der Schaltung selbst ausreichen, um die Amplitude zu begrenzen (Arbeitspunktverschiebung, Begrenzung an nichtlinearen Kennlinien, Abnahme der Spannungsverstärkung bei Zunahme der Amplitude).

Die frequenzbestimmenden Bauteile elektronischer Oszillatoren können sein:

• Spulen und Kondensatoren im Schwingkreis
• RC-Glieder bzw. Tiefpässe beim RC-Oszillator (Niederfrequenz)
• Laufzeiten in elektronischen Bauteilen beim Ringoszillator
• Topfkreise, Hohlraumresonatoren und Lecherleitungen im Dezimeter- und Zentimeterwellen-Bereich
• Schwingquarze, Keramikresonatoren im oberen Kilohertz- bis zweistelligem Megahertz-Bereich
• Oberflächenwellen
• Yttrium-Eisen-Granat-Kristalle (Elektronenspinresonanz), siehe YIG-Filter (Zentimeterwellen)
• winzige mechanische Schwinger im MEMS-Oszillator

Beispiele (Auswahl)

Weblinks

Wiktionary: Oszillator  – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Periodic Orbit - Scholarpedia

Einzelnachweise

1. ↑ Mechanische Schwingungen. In: LEIFIphysik. Abgerufen am 24. Juni 2020. 
2. ↑ oscillate: definition of oscillate in Oxford dictionary (British & World English)
3. 1 2 Jeff Moehlis et al.: Periodic Orbit. In: Scholarpedia. 2006, doi:10.4249/scholarpedia.1358. 
4. 1 2 3 Gerd Simon Schmidt: Synchronization of Oscillators and Global Output Regulation for Rigid Body Systems. Logos Verlag Berlin, 2014, ISBN 3-8325-3790-2, S. 11–16 (eingeschränkte Vorschau in der Google-Buchsuche). 
5. ↑ Niklas Luhmann, Organisation und Entscheidung (Opladen [u. a.]: Westdt. Verl., 2000). S. 224
6. 1 2 F. Ventriglia (Hrsg.): Neural Modeling and Neural Networks. Elsevier, 2013, ISBN 1-4832-8790-4, S. 80 (eingeschränkte Vorschau in der Google-Buchsuche).