Satz von Pythagoras#
von Arnela Blazevic, Carina Fasching, Nah-Rah Han; BG/BRG Pestalozzi, 7b; Betreuung: Camhy; 80 Punkte;
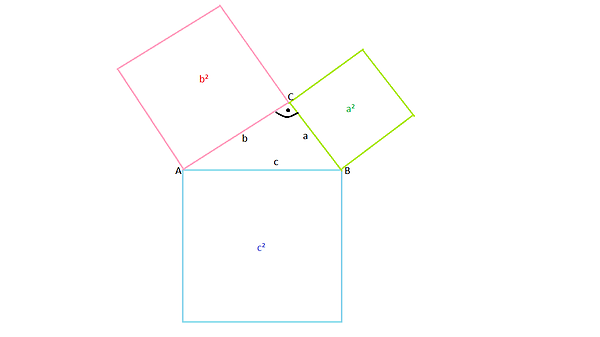
I. Zusammenhang zwischen den Seiten rechtwinkeliger Dreiecke: In jedem Dreieck ist der Flächeninhalt des Quadrates über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten. Dabei werden die Katheten mit a und b benannt, sowieso die Hypotenuse mit c. So lässt sich der Satz des Pythagoras durch die Gleichung a² + b² = c² angeben.
Obwohl der Name des Lehrsatzes auf Pythagoras von Samos zurückgeht, gab es schon lange vor der Antike vergleichbare Aussagen, nämlich im Babylonischen Reich. Um 3000 v. Chr. gab es wesentliche Bestandteile einer mathematischen Theorie, in denen die Aussage des Satzes des Pythagoras enthalten war.
II. Beweise für den Satz:
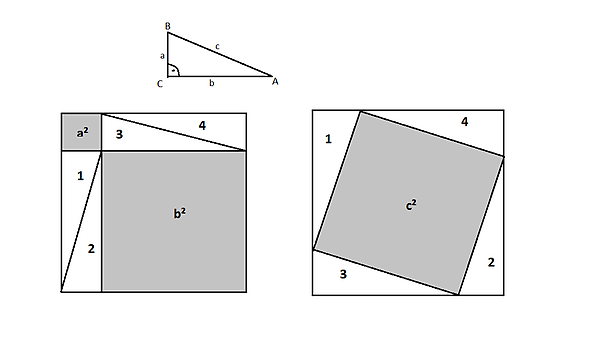
400 verschiedene Beweise bekannt. Beide Quadrate haben jeweils die Seitenlänge a+b und deshalb gleiche Flächeninhalte (a+b)². Beide Quadrate enthalten jeweils 4mal das Dreieck ABC.
Die weißen Flächen haben in beiden Quadraten jeweils den gleichen Flächeninhalt. Daher müssen die Flächeninhalte der grauen Flächen auch gleich sein. Weil der Flächeninhalt des linken Bildes a² + b² (graue Flächen) beträgt und der Flächeninhalt von c² (rechtes Bild) gleich groß ist, ergibt sich folgende GleichungDie Flächen, die ans Dreieck anschließen, müssen nicht zwingend Quadrate sein, sondern es können auch beliebige Figuren (ähnliche Dreiecke, Kreise, ...) sein, solange ihre Fläche jeweils proportional zum Quadrat der Seite mit einem entsprechenden Proportionalitätsfaktor ungleich Null ist ( ta2 + tb2 = tc2 ).
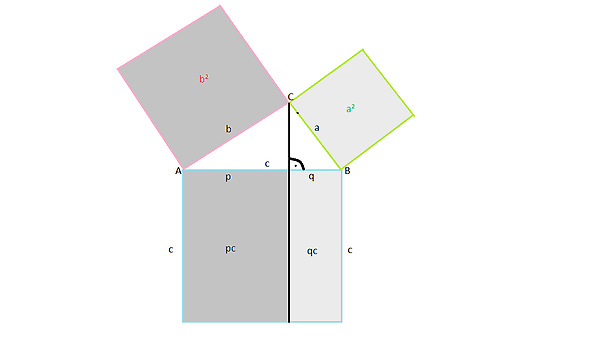
Das ist darum so wichtig, weil viele Menschen glauben, der pythagoräische Lehrsatz habe mit der Form "Quadrat" zu tun: er hat aber nur mit der "zweiten Potenz" zu tun, und und nur weil wir meistens "a Quadrat" statt "a zur zweiten Potenz" sagen, prägt sich bei uns der Gedanke ein, dass es um die Form "Quadrat" geht!III. Die Satzgruppe des Pythagoras Diese Satzgruppe ist eng verwandt mit dem Kathetensatz (Euklid). In jedem rechtwinkeligen Dreieck hat das Quadrat über einer Kathete den gleichen Flächeninhalt wie das Rechteck, das aus der Hypotenuse und dem der Kathete zugehörigen Hypotenusenabschnitt gebildet wird.
Mit den Bezeichnungen aus Abb. 3 gilt also: a²=q∙c und b²=p∙c Der Satz des Pythagoras sowie der Höhen- und der Kathetensatz werden oft zusammenfassend als Gruppe des Pythagoras bezeichnet. Dieser kann dabei mit Hilfe des Kathetensatzes nachgewiesen werden. Aus a² = q∙c und b² = p∙c folgt nämlich: a²+b²=q∙c+p∙c=(q+p)∙c=c²
IV. Anwendungen des Satzes
• Anwendungen im Alltag: Bildschirmdiagonale eines Fernsehers, die Höhe einer Leiter, Entfernung in Luftlinie usw.
• Die Länge der Diagonalen eines Rechtecks oder die Länge der Raumdiagonalen eines Quaders
• Abstand zweier Punkte einer Ebene oder des Raumes
V. Die Umkehrung des Satzes von Pythagoras: Ein Zusammenhang zwischen den Seitenlängen besteht nur in rechtwinkeligen Dreiecken: Wenn für die Seitenlänge a, b und c eines Dreiecks die Gleichung a² + b² = c² erfüllt ist, so ist dieses Dreieck rechtwinklig und c ist eine Hypotenuse. Mit dieser Umkehrung lässt sich ermitteln, ob ein Dreieck rechtwinklig ist. Z.B.: Die Harpedonapten wendeten 2300 v.Chr. pythagoräische Dreiecke an, um nach Überschwemmungen des Nils die Ländereien wieder rechtwinklig abzustecken.
VI. Verallgemeinerungen des Satzes von Pythagoras: Die bekannteste Verallgemeinerung des Satzes ist der Kosinussatz. Ist ein Dreieck rechtwinklig, so ist der Kosinus eines der Winkel 0 und die Gleichung c² = a² + b² - 2ab ∙ cos(γ) des Kosinussatzes nimmt die Gestalt des Satzes von Pythagoras an. Der Winkel gegenüber der Seite c muss 90° sein, damit dieser ein rechter Winkel ist.
VII. Pythagoräische Zahlentripel:
Ein pythagoräischer Tripel ist ein Tripel (a; b; c) dreier natürlicher Zahlen, für die gilt a²+b²=c².
Die bekanntesten Tripel sind (3; 4; 5), (6; 8; 10); (5; 12; 13); (8; 15; 17).
Ein Dreieck mit solchen Seitenlängen ist rechtwinkelig.
Werden alle drei Zahlen eines pythagoräischen Zahlentripels mit derselben natürlichen Zahl k multipliziert, so entsteht natürlich wieder ein pythagoräisches Zahlentripel, denn es gilt (ka)²+ (kb)²= k²*(a²+b²)= (kc)². Daraus ergibt sich, dass es unendlich viele Zahlentripel gibt. Freilich beschreiben diese Zahlentripel verschieden große, aber immer zueinander ähnliche Dreiecke.
"Interessantere" Pythagoräischen Tripel erhält man, indem man beliebige natürliche Zahlen u und v mit u>v wählt und Tripel (u2 - v2, 2uv, u2 + v2. Das gibt mit kleinen Änderungen (Kürzung durch gemeinsame Teiler) auch alle möglichen Tripel. Beispiel: u=5, v=3 ergibt (16,30,34) ein Tripel, durch gemeinsamen Teiler 2 dividiert (8,15,17), ein weiteres, und mit u=5, v=4 und u=7, v=6 (9,40,41) bzw. (13,84,85), sehr "schmale" rechtwinkelige Dreiecke: setzt man das fort, nimmt man also u=2n+1, v=2n so erhält man Tripel (4n+1, 8n2 + 4n, 8n2 +4n+ 1), also Dreiecke, wo sich Hypothenuse und Kathete immer nur um 1 unterscheiden.
Hier noch eines der Videos, die den Satz des Pythagoras erklären. http://www.youtube.com/watch?v=xg6t2jo6MHY
Recherche#
- Quelle 1: Bartels, Hans-Jochen u.a.: Lexikon der Mathematik. 4. Band. Spektrum Akademischer Verlag, Berlin 2002.
- Quelle 2: Fraedrich, Anna M.: Die Satzgruppe des Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994.
- Quelle 3: Schupp Hans: Elementargeometrie. UTB, Stuttgart 1977.
- Quelle 4: Eines der vielen YouTube Videos die den Satz erklären