Binomialkoeffizient
Der Binomialkoeffizient ist eine mathematische Funktion, mit der sich eine der Grundaufgaben der Kombinatorik lösen lässt, nämlich auf wie viele verschiedene Arten man aus einer Menge von verschiedenen Objekten jeweils Objekte auswählen kann (ohne Zurücklegen und ohne Beachtung der Reihenfolge). Der Binomialkoeffizient ist also die Anzahl der -elementigen Teilmengen in der Potenzmenge einer -elementigen Grundmenge.
„49 über 6“ in Deutschland bzw. „45 über 6“ in Österreich und der Schweiz ist z. B. die Anzahl der möglichen Ziehungen beim Lotto (ohne Berücksichtigung der Zusatzzahl).
Ein Binomialkoeffizient hängt von zwei nichtnegativen ganzen Zahlen und ab. Er wird mit dem Symbol
geschrieben und als „n über k“, „k aus n“ oder „n tief k“ gesprochen. Die englische Abkürzung nCr für n choose r findet sich als Beschriftung auf Taschenrechnern.
Den Namen erhielten diese Zahlen, da sie als Koeffizienten in den Potenzen des Binoms auftreten; es gilt der sogenannte binomische Lehrsatz:
Eine Erweiterung des aus der Kombinatorik stammenden Binomialkoeffizienten stellt der allgemeine Binomialkoeffizient dar, der in der Analysis verwendet wird.
Definition
Für ganze Zahlen ist der Binomialkoeffizient „n über k“ auf folgende Weise definiert:
wobei die Fakultät von bezeichnet. Das leere Produkt () ist dabei . Für setzt man zudem .
Eigenschaften
Einfache Rechenregeln
Unmittelbar aus der Definition ergeben sich für die Umformungen:
Über das Wegkürzen der Fakultäten können damit auch Binomialkoeffizienten mit großen Werten in annehmbarer Zeit berechnet werden. Es gilt weiter:
- ist stets eine nichtnegative ganze Zahl. Ist , so ist , anderenfalls ist .
- . Für ist der rechte Summand .
Symmetrie
Ganzzahlige Binomialkoeffizienten sind symmetrisch im Sinne von
für alle nichtnegativen und .
- Beweis
- Beispiel
Rekursive Darstellung und Pascalsches Dreieck
Für ganze Zahlen und mit lassen sich die Binomialkoeffizienten auch durch folgende Rekursionsvorschrift ermitteln:
- für alle
- für alle und für alle mit
Mit ihrer Hilfe lassen sich leicht alle Binomialkoeffizienten bis zu einer vorgegebenen Schranke für bestimmen, ein Schema dafür ist das Pascalsche Dreieck: Der rekursive Teil entspricht dort der Tatsache, dass jede Zahl die Summe der beiden über ihr stehenden Zahlen ist.
- Beweis
Den Koeffizienten findet man dabei in der -ten Zeile an der -ten Stelle (beide ab Null gezählt!):
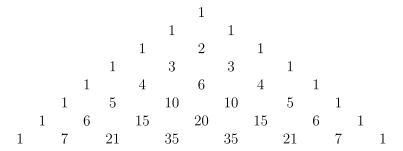
Das gleiche Dreieck dargestellt in den -Binomialsymbolen:
Algorithmus zur effizienten Berechnung
Für ganzzahlige existiert ein effizienter Algorithmus, der die Produktformel
des Binomialkoeffizienten anwendet. Auf Grund des stetigen Wechsels zwischen Multiplikation und Division wachsen die Zwischenergebnisse nicht unnötig an. Zusätzlich sind auch alle Zwischenergebnisse natürliche Zahlen.
Um unnötigen Rechenaufwand zu vermeiden, berechnet man im Fall den Binomialkoeffizienten:
Der folgende Pseudocode verdeutlicht die Berechnung:
binomialkoeffizient(n, k) 1 wenn 2*k > n dann k = n-k 2 ergebnis = 1 3 für i = 1 bis k 4 ergebnis = ergebnis * (n + 1 - i) / i 5 rückgabe ergebnis
Diese Rechenmethode nutzen auch Taschenrechner, wenn sie die Funktion anbieten. Sonst wäre die Rechenkapazität oftmals für erschöpft, da . Die Beschriftung der Funktionstaste mit nCr beschreibt die Reihenfolge der Eingabewerte in Infixnotation; zunächst Anzahl der Elemente n, dann die Funktionstaste Combinations, dann Anzahl der gewählten Objekte r (im Artikel mit k bezeichnet).
Die Berechnung nPr (engl. Permutations) berücksichtigt die Permutationen der r Elemente, die Division durch unterbleibt:
- .
Der Binomialkoeffizient in der Kombinatorik
In der abzählenden Kombinatorik gibt
die Anzahl der Kombinationen ohne Wiederholung von Elementen aus Elementen an. Durch diese Eigenschaft spielt der Binomialkoeffizient eine zentrale Rolle in der Kombinatorik und findet Eingang in die Berechnung und in die Formeln anderer kombinatorischer Größen.
Veranschaulichung mit Mengen
Vergleiche auch: Kombination (Kombinatorik) → Mengendarstellung
Eine andere Interpretation von Kombinationen ohne Wiederholung von k aus n Elementen ist die Anzahl aller -elementigen Teilmengen einer -elementigen Menge.
Sie kann anschaulich etwa so gedeutet werden:
Variante 1
Zunächst zählt man alle -Tupel mit paarweise verschiedenen Elementen, die sich aus der -elementigen Ausgangsmenge zusammenstellen lassen. Es gibt Möglichkeiten der Wahl des ersten Tupel-Elements. Nach jeder beliebigen Wahl dieses ersten gibt es nur noch Wahlmöglichkeiten für das zweite Element, nach dessen Wahl nur noch für das dritte usw., bis hin zu Wahlmöglichkeiten für das -te und letzte Tupel-Element. Die Anzahl aller so zusammengestellten -Tupel ist also das Produkt von Faktoren, das sich mit Hilfe der Fakultät auch als notieren lässt. Nun sind aber genau je der gezählten -Tupel Permutationen voneinander und entsprechen daher ein und derselben -elementigen Teilmenge. Nach Division durch diese „Zähl-Vielfachheit“ ergibt sich also tatsächlich als die gesuchte Teilmengenanzahl.
Variante 2
Eine andere, symmetrischere Veranschaulichung betont nicht den Akt der Auswahl von aus Elementen, sondern den Aspekt der Zerlegung in zwei Teilmengen aus und Elementen. Angenommen, ein -elementiges Ausgangstupel bestehe aus roten und weißen irgendwie aufgereihten Elementen. Bildet man alle Permutationen dieser Aufreihung, so sind je davon farblich ununterscheidbar, denn je Permutationen der roten Elemente untereinander ändern nichts an der Farbsequenz, ebenso wenig wie je davon unabhängige Permutationen innerhalb der weißen. Es gibt also nur farblich verschiedene Sequenzen der Länge mit allen möglichen unterschiedlichen Belegungen durch je rote Elemente. Jede Sequenz lässt sich nun aber eineindeutig einer der -elementigen Teilmengen einer -elementigen Menge zuordnen. Dasselbe gilt wegen der Symmetrie von rot und weiß oder von und auch für die komplementären -elementigen Teilmengen. Die Gesamtzahl dieser Teilmengen ist damit je .
Erstes Beispiel
Für die Anzahl der möglichen Ziehungen oder Tippscheine beim deutschen Lotto 6 aus 49 (ohne Zusatzzahl oder Superzahl) gilt:
Es gibt hier offensichtlich genau eine Möglichkeit, 6 Richtige zu tippen. zählt die Möglichkeiten für 0 Richtige, nämlich alle 6 Tipps aus den 43 Falschen zu wählen. Die Anzahl verschiedener Tipps mit 5 Richtigen ergibt sich zu , denn es gibt 6 Möglichkeiten, nur 5 der 6 gezogenen Zahlen zu tippen (oder eine davon auszulassen), und dann jeweils Möglichkeiten, den ausgelassenen Tipp auf eine der 43 falschen Zahlen zu setzen. Allgemein ergibt sich die Anzahl der verschiedenen Tipps mit Richtigen bei 6 aus 49 mit derselben Überlegung zu . Bei 6, 0 und 5 Richtigen fällt kaum auf, dass die verwendeten Faktoren , und eigentlich einfache Binomialkoeffizienten sind. Die Summe aller genannten Tippzahlen ergibt die Gesamtzahl 13983816 aller möglichen Tipps – das folgt aus der unten angegebenen Vandermondeschen Identität.
Die Wahrscheinlichkeit für 6 mit einem Tipp erzielte Richtige ist also , die für 5 Richtige ist . Für 0 Richtige ergeben sich mit schon etwa 44 %. Die allgemeine Wahrscheinlichkeit für Richtige ist ein Spezialfall der hypergeometrischen Verteilung, die gerade drei Binomialkoeffizienten derart kombiniert.
Zweites Beispiel
Ein weiteres Beispiel behandelt einen Sack voller farbiger Murmeln. Die Wahrscheinlichkeit, dass aus insgesamt roten, grünen und blauen Murmeln genau rote, grüne und blaue Murmeln gezogen werden, wobei insgesamt Murmeln herauszunehmen sind, hat folgenden Wert:
Wenn beispielsweise aus einem Murmelsack mit insgesamt roten, grünen und blauen Murmeln genau sechs Murmeln blind herausgenommen werden sollen, dann beträgt die Wahrscheinlichkeit, dass sich unter den sechs herausgenommenen Murmeln genau rote, grüne und blaue Murmeln befinden, exakt :
Weitere Beispiele siehe unter: Kombination (Kombinatorik) → Beispiele
Kombinatorische Beweise
Die kombinatorische Deutung erlaubt auch einfache Beweise von Relationen zwischen Binomialkoeffizienten, etwa durch doppeltes Abzählen. Beispiel: Für gilt:
Beweis: Es sei eine -elementige Menge und ein festes Element. Dann zerfallen die -elementigen Teilmengen von in zwei Klassen:
- die Teilmengen, die enthalten; sie bestehen also aus zusammen mit einer -elementigen Teilmenge der -elementigen Menge ,
- die Teilmengen, die nicht enthalten; sie sind -elementige Teilmengen der -elementigen Menge .
Kombinationsmengen
Die Menge aller -elementigen Teilmengen einer Menge wird wegen ihrer Mächtigkeit gelegentlich auch mit bezeichnet. Damit gilt für jede endliche Menge :
Ausdrücke mit Binomialkoeffizienten
Summen mit Binomialkoeffizienten
Dieser Formel liegt ein kombinatorischer Sachverhalt zu Grunde. Da die Anzahl aller -elementigen Teilmengen einer -elementigen Menge ist, ergibt sich durch die Summation die Anzahl aller ihrer Teilmengen, also . Die Formel lässt sich auch aus dem binomischen Lehrsatz herleiten, indem man setzt.
Summen mit alternierenden Binomialkoeffizienten
- für .
Diese Formel folgt für ungerade aus der Symmetrie des Binomialkoeffizienten. Für beliebige lässt sie sich aus dem binomischen Lehrsatz herleiten, indem und (oder und ) gesetzt wird.
Summen von Binomialkoeffizienten mit geraden bzw. ungeraden Anzahlen ausgewählter Objekte
Durch Subtraktion bzw. Addition obiger Gleichungen und und anschließende Halbierung ist für zu erhalten:
wie auch ;
hierbei sind Gaußklammern.
Summe verschobener Binomialkoeffizienten
Ausgehend vom Induktionsanfang für beliebiges , der die Rekursionsvorschrift für Binomialkoeffizienten nutzt, ist mit Induktion nach unter erneuter Nutzung der Rekursionsvorschrift leicht zu beweisen:
- ;
wegen Symmetrie der Summanden wie auch der Summe gilt ebenso:
- .
Vandermondesche Identität
Es gibt auch hier ein kombinatorisches Argument: Die rechte Seite entspricht der Anzahl von -elementigen Teilmengen einer -elementigen Menge von Kugeln. Man kann sich nun vorstellen, dass die Kugeln zwei verschiedene Farben haben: Kugeln seien rot und Kugeln grün. Eine -elementige Teilmenge besteht dann aus einer gewissen Anzahl von roten Kugeln und vielen grünen. Für jedes mögliche gibt der entsprechende Summand auf der linken Seite die Anzahl der Möglichkeiten für solch eine Aufteilung in rote und grüne Kugeln an. Die Summe liefert die Gesamtzahl. Ein oft als einfacher empfundener Beweis verwendet den Binomischen Lehrsatz in der Form
sowie den Ansatz
und Koeffizientenvergleich.
Im Spezialfall ergibt sich aus der Vandermondeschen Identität folgende Formel für die Quadratsummen:
Mit dem Kürzel wird der Mittlere Binomialkoeffizient (Zentralbinomialkoeffizient, Central Binomial Coefficient) gekennzeichnet.
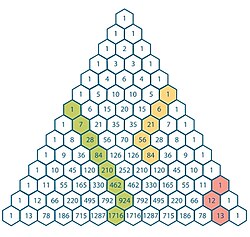
Hockey-Stick-Identität
Für mit gilt . Der Name Hockey-Stick-Identität (Hockeyschläger-Identität) rührt von der graphischen Darstellung der Identität auf dem Pascalschen Dreieck her: Wenn die einzelnen Summanden und der Wert der Summe selbst farblich hervorgehoben werden, erinnert die Form an einen Hockeyschläger.
Fibonacci-Zahlen
Die Fibonacci-Zahlenfolge ist eine unendliche Folge aus natürlichen Zahlen, welche zweimal mit der Zahl Eins beginnt und bei jede Zahl als Summe der beiden in der Folge vorangehenden Zahlen entsteht. Es gilt also , und für stets .
Mit den Binomialkoeffizienten können die Fibonaccizahlen in Form einer geschlossenen Summe dargestellt werden:
Beispielsweise gilt für diese Fibonacci-Zahlen aus den ungeraden Indizes:
Und es gilt für jene Fibonacci-Zahlen aus den geraden Indizes:
Zentraler Grenzwertsatz
Die Mathematiker Jarl Waldemar Lindeberg und Paul Pierre Lévy erkannten, dass bei der additiven Überlagerung unendlich vieler kleiner unabhängiger Zufallseffekte zu einem Gesamteffekt die Gaußsche Normalverteilung ergibt. Der Binomialkoeffizient ist für Zahlenpaare a und b jenseits von den natürlichen Zahlen auf folgende Weise definiert:
Dabei bezeichnet die Gammafunktion. Mit dieser kontinuierlichen Definition des Binomialkoeffizienten gilt somit der zentrale Grenzwertsatz:
Gemäß diesem Satz ergibt die infinitesimale Annäherung der Binomialkoeffizientenfunktion nach dem soeben beschriebenen Muster die Gaußsche Glockenkurvenfunktion.
Divisionsreste
Ist eine Primzahl, und , dann ist
Das heißt, modulo kann mit Hilfe der Darstellungen von und zur Basis effizient berechnet werden, nämlich „ziffernweise“.
Binomialkoeffizienten in der Analysis
Verallgemeinerung
Komplexe Verallgemeinerung
Wie bereits im Definitionsteil genannt, so lautet die generelle Verallgemeinerung für positive obere Einträge und für reelle untere Einträge wie folgt:
Eine weitere Verallgemeinerung, die in der Analysis eine Rolle spielt, erhält man, wenn man für den oberen Eintrag eine beliebige komplexe Zahl zulässt, aber den unteren Eintrag weiterhin als ganzzahlig voraussetzt, durch die Definition
Man spricht auch vom allgemeinen Binomialkoeffizienten „ über “. Diese Definition stimmt für nichtnegative ganzzahlige mit der kombinatorischen Definition (also der Definition von als die Anzahl aller -elementigen Teilmengen einer -elementigen Menge) überein, und für nichtnegative mit der algebraischen Definition (also der Definition von als das Produkt ).
Anwendung für algebraisch darstellbare Fälle
Beispielsweise ist
und
Auch der zweite Parameter lässt sich auf beliebige komplexe Belegung verallgemeinern, wenn mit Hilfe der Betafunktion für definiert wird:
wobei die Gammafunktion bezeichnet. Ist dabei oder eine negative ganze Zahl, so ist der Wert der rechten Seite 0, weil die nichtpositiven ganzen Zahlen die (einzigen) Polstellen von sind.
Ersichtlich gilt weiterhin die Symmetriebeziehung
- ,
insbesondere
- ,
Anwendung für negativzahlige Einträge
und bei nichtnegativem ganzen
- .
Um das Vorzeichen aus dem ersten Parameter zu extrahieren, sofern er ganzzahlig ist, lässt sich die Relation
angeben.
Allgemein gilt für komplexe , die Beziehung
- .
Eine weitere Verallgemeinerung bieten die Multinomialkoeffizienten, die bei der Verallgemeinerung des binomischen auf den multinomialen Lehrsatz benötigt werden.
Binomische Reihen
Für und mit erhält man die Beziehung
die eine Verallgemeinerung der geometrischen Reihe darstellt und zu den binomischen Reihen gehört.
Ist , sowie , konvergiert die folgende Reihe gemäß
Exaktere Bedingungen für und sind im Artikel Binomische Reihe angegeben.
Wurzelbrüche
Für und erhält man die folgende Beziehung:
Dieser Ausdruck kann alternativ so mit der Gammafunktion dargestellt werden:
Summenausdruck für die Betafunktion
Eine weitere Beziehung kann man für alle relativ einfach mit vollständiger Induktion beweisen,
woraus unmittelbar die Symmetrie
folgt. Eine Verallgemeinerung für mit und lautet
Gaußsche Produktdarstellung für die Gammafunktion
Mit der letzten Formel aus dem vorherigen Abschnitt ist für
Betrachtet man den Fall , ersetzt die Brüche in der Summe durch Integrale gemäß
und fasst die Summe der Potenzen den binomischen Formeln entsprechend zusammen, erhält man
wobei beim letzten Integral die Substitution angewendet wurde. Schließlich hat man die Gleichung
woraus sich durch den Grenzübergang direkt die Gaußsche Produktdarstellung der Gammafunktion,
ergibt.[2]
Digammafunktion und Euler-Mascheroni-Konstante
Für mit gilt
was sich ebenfalls über Induktion nach beweisen lässt. Für den Spezialfall vereinfacht sich diese Gleichung zu
wobei die Folge der Harmonischen Zahlen, also der Partialsummen der Harmonischen Reihe ist. Die Umwandlung der linken Summe in eine Reihe (Limit statt ) ist dabei erlaubt wegen für
ist andererseits darstellbar als
mit der Digammafunktion und der Euler-Mascheroni-Konstanten
kann auf komplexe Werte – außer auf negative ganze Zahlen – fortgesetzt werden. Man bekommt so die Reihe
als komplexe Interpolation der Folge der Harmonischen Zahlen.
Trivia
Die wörtliche Übersetzung von „ über “ ins Englische „ over “ bezeichnet nicht den Binomialkoeffizienten , sondern den Bruch . Korrekt ist „ choose “.
Weblinks
- Download von BigAl. (Kleines, freies und plattformunabhängiges Programm, u. a. zur genauen Berechnung des Binomialkoeffizienten; mit Quelltext).
- Online-Berechnung von Binomialkoeffizienten.
- Christoph Pöppe: Wie findet man acht Richtige aus elf? in Spektrum.de vom 6. Dezember 2022
Einzelnachweise
- ↑ Vandermonde's Identity | Brilliant Math & Science Wiki. Abgerufen am 29. Januar 2025 (amerikanisches Englisch).
- ↑ Disquisitiones generales circa seriem infinitam 1+…. 1813, S. 26 (auch in Carl Friedrich Gauß: Werke. Band 3, S. 145).
License Information of Images on page#
| Image Description | Credit | Artist | License Name | File |
|---|---|---|---|---|
| The Wikimedia Commons logo, SVG version. | Original created by Reidab ( PNG version ) SVG version was created by Grunt and cleaned up by 3247 . Re-creation with SVG geometry features by Pumbaa , using a proper partial circle and SVG geometry features. (Former versions used to be slightly warped.) | Reidab , Grunt , 3247 , Pumbaa | Datei:Commons-logo.svg | |
| Graphic illustration of the "Hockey Stick Identity" showing the sum of "n" elements on a diagonal in Pascal's Triangle. | https://math.stackexchange.com/questions/1490794/proof-of-the-hockey-stick-identity-sum-limits-t-0n-binom-tk-binomn1 | hlapointe | Datei:Identidad del palo de hockey.jpg | |
| Illustration of Pascal's triangle up to row 7 | Eigenes Werk | Rohieb | Datei:Pascal triangle small.svg | |
| Wikibooks logo; Favicon is | Eigenes Werk | Bastique , Ramac et al. | Datei:Wikibooks-logo.svg | |
| Datei:Wiktfavicon en.svg |


































![{\displaystyle {\begin{aligned}{\binom {n}{k}}+{\binom {n}{k+1}}&={\frac {n!}{k!\cdot (n-k)!}}+{\frac {n!}{(k+1)!\cdot (n-(k+1))!}}\\[.5em]&={\frac {(k+1)\cdot n!}{(k+1)\cdot k!\cdot (n-k)!}}+{\frac {n!\cdot (n-k)}{(k+1)!\cdot (n-k-1)!\cdot (n-k)}}\\[.5em]&={\frac {(k+1)\cdot n!}{(k+1)!\cdot (n-k)!}}+{\frac {n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {(k+1)\cdot n!+n!\cdot (n-k)}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {n!\cdot ((k+1)+(n-k))}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {n!\cdot (n+1)}{(k+1)!\cdot (n-k)!}}\\[.5em]&={\frac {(n+1)!}{(k+1)!\cdot ((n+1)-(k+1))!}}\\[.5em]&={\binom {n+1}{k+1}}\end{aligned}}}](/aw/img/svg/740452fe9a2ea07ef8c1d9c99f5f1653155926aa)



















































































































































































