Stirlingformel

Die Stirling-Formel ist eine mathematische Formel, mit der man für große Fakultäten Näherungswerte berechnen kann. Sie ist benannt nach dem Mathematiker James Stirling.

Grundlegendes

Die Stirling-Formel in ihrer einfachsten Form ist eine asymptotische Formel

${\displaystyle n!\simeq {\sqrt {2\pi n}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n},\qquad n\to \infty }$

Zu den einzelnen Elementen dieser Formel siehe Fakultät (!), Quadratwurzel (√), Kreiszahl (π) und Eulersche Zahl (e).

Eine Ableitung findet sich im Artikel Sattelpunktsnäherung.

Genauer gilt für ${\displaystyle n>0}$ :

${\displaystyle 1<\mathrm {e} ^{1/(12n+1)}\leq {\frac {n!}{{\sqrt {2\pi n}}\cdot ({\frac {n}{\mathrm {e} }})^{n}}}\leq \mathrm {e} ^{1/(12n)}<1+{\frac {1}{11n}}}$

Insbesondere ist der Grenzwert des Bruches für ${\displaystyle n\to \infty }$ gleich 1.

Die Stirling-Reihe für ${\displaystyle \ln(n!)=\sum _{i=1}^{n}\ln(i)}$ nach der Euler-MacLaurinschen Summenformel lautet

${\displaystyle \ln(n!)\approx n\ln(n)-n+{\tfrac {1}{2}}\ln(2\pi n)+{\frac {1}{12n}}-{\frac {1}{360n^{3}}}+\cdots +{\frac {B_{2k}}{(2k-1)2k}}\cdot {\frac {1}{n^{2k-1}}}+\cdots ,}$

wobei ${\displaystyle B_{k}}$ die k-te Bernoulli-Zahl bezeichnet. Als Näherung betrachtet man lediglich eine endliche Zahl von Gliedern. Der Fehler liegt in der Größenordnung des ersten vernachlässigten Gliedes. Beispiel: bricht man nach dem dritten Glied ab, ist der absolute Fehler kleiner als ${\displaystyle 1/(12n)}$ . Die Reihe selbst konvergiert nicht für festes n, sie ist eine asymptotische Entwicklung.

Für n > 7,31×10⁴³ genügt ein Glied für einen relativen Fehler kleiner als 1 Prozent:

${\displaystyle \ln(n!)\approx n\cdot \ln(n)}$

Für ${\displaystyle n>751}$ genügen zwei Glieder für einen relativen Fehler kleiner als 0,1 Prozent:

${\displaystyle \ln(n!)\approx n\cdot \ln(n)-n}$

Für kleine n lässt sich aus der Formel für drei Glieder eine einfache Formel für n! ableiten. Mit

${\displaystyle {\mathrm {e} }^{1/(12n)}\approx 1+{\frac {1}{12n}}\approx {\sqrt {1+{\frac {1}{6n}}}}}$

ergibt sich die Approximation

${\displaystyle n!\approx {\sqrt {2\pi n}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n}\;{\mathrm {e} }^{1/(12n)}\approx {\sqrt {2\pi n}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n}{\sqrt {1+{\frac {1}{6n}}}}={\sqrt {{\pi \over 3}(6n+1)}}\;\left({\frac {n}{\mathrm {e} }}\right)^{n}}$

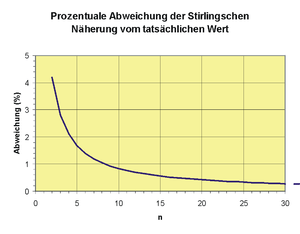
Der Fehler ist (bei minimalem zusätzlichem Rechenaufwand zur Berechnung der ersten beiden Glieder) kleiner als 3 % für n = 0, kleiner als 1 % für n > 0 und kleiner als 0,1 % für n > 2.

Durch Einsetzen in die Exponentialfunktion ergibt sich für ${\displaystyle n!}$ :

${\displaystyle n!\approx n^{n}\cdot {\sqrt {2\pi n}}\cdot \mathrm {e} ^{-n+{\frac {1}{12n}}-{\frac {1}{360n^{3}}}+\cdots +{\frac {B_{2k}}{(2k-1)2k}}\cdot {\frac {1}{n^{2k-1}}}+\cdots },}$

und durch Einsetzen der Stirlingschen Reihe in die Reihe der Exponentialfunktion:

${\displaystyle n!=n^{n}\cdot {\sqrt {2\pi n}}\,\cdot \,\mathrm {e} ^{-n}\,\cdot \,\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots +{\frac {C_{k}}{n^{k}}}+\cdots \right),}$

wobei die Koeffizienten ${\displaystyle C_{k}}$ keinem einfachen Bildungsgesetz genügen.

Verallgemeinerung: Stirling-Formel für die Gammafunktion

Für alle ${\displaystyle x>0}$ gilt

${\displaystyle \Gamma (x)={\sqrt {2\pi /x}}\,\left({\frac {x}{\mathrm {e} }}\right)^{x}\,\mathrm {e} ^{\mu (x)}}$ ,

wobei ${\displaystyle \mu }$ eine Funktion ist, die ${\displaystyle 0<\mu (x)<1/(12x)}$ für alle ${\displaystyle x>0}$ erfüllt.

Zu den einzelnen Elementen dieser Formel siehe Gammafunktion ( ${\displaystyle \Gamma }$ ), Quadratwurzel (√), Kreiszahl (π) und Eulersche Zahl (e).

Für alle ${\displaystyle x>0}$ ist der Wert einer Approximation von ${\displaystyle \Gamma (x)}$ nach obiger Formel mit ${\displaystyle \mu =0}$ also immer etwas zu klein. Der relative Fehler ist aber für x ≥ 9 kleiner als 1 % und für x ≥ 84 kleiner als 0,1 %.

Es gilt für alle ${\displaystyle n\in \mathbb {N} }$

${\displaystyle n!=n\Gamma (n)=n{\sqrt {2\pi /n}}\,\left({\frac {n}{\mathrm {e} }}\right)^{n}\,\mathrm {e} ^{\mu (n)}={\sqrt {2\pi n}}\,\left({\frac {n}{\mathrm {e} }}\right)^{n}\,\mathrm {e} ^{\mu (n)}}$ ,

womit sich als Spezialfall die Approximationsformeln des vorigen Abschnitts ergeben.

Anwendungen

Die Stirling-Formel findet überall dort Verwendung, wo die exakten Werte einer Fakultät nicht von Bedeutung sind. Insbesondere bei der Berechnung der Information einer Nachricht und bei der Berechnung der Entropie eines statistischen Ensembles von Subsystemen ergeben sich mit der Stirling-Formel starke Vereinfachungen.

Beispiel: Gegeben sei ein System mit ${\displaystyle N}$ verschiedenen Subsystemen, von denen jedes ${\displaystyle m}$ verschiedene Zustände annehmen kann. Ferner sei bekannt, dass der Zustand ${\displaystyle i}$ mit der Wahrscheinlichkeit ${\displaystyle \omega _{i}}$ angenommen werden kann. Damit müssen sich ${\displaystyle N_{i}}$ Subsysteme im Zustand ${\displaystyle i}$ befinden und es gilt ${\displaystyle N_{i}/N=\omega _{i}}$ . Die Zahl der möglichen Verteilungen eines so beschriebenen Systems beträgt dann

${\displaystyle N!/(N_{1}!\,N_{2}!\,\ldots \,N_{m}!)}$

und für dessen Entropie ${\displaystyle \sigma }$ gilt

${\displaystyle \sigma =\ln(N!)-\ln(N_{1}!)-\ldots -\ln(N_{m}!).}$

Mittels der Stirling-Formel kann man nun bis auf Fehler der Ordnung ${\displaystyle O(\ln(N))}$ diese Formel vereinfachen zu

${\displaystyle \sigma \,}$	${\displaystyle =N(\ln N-1)-N_{1}(\ln N_{1}-1)-\ldots -N_{m}(\ln N_{m}-1)}$
	${\displaystyle =N\ln N-N_{1}\ln N_{1}-\ldots -N_{m}\ln N_{m}}$
	${\displaystyle =(N_{1}+\ldots +N_{m})\ln N-N_{1}\ln N_{1}-\ldots -N_{m}\ln N_{m}}$
	${\displaystyle =-N_{1}\ln(N_{1}/N)-\ldots -N_{m}\ln(N_{m}/N)}$
	${\displaystyle =-N\sum _{i=1}^{m}(\omega _{i}\ln \omega _{i})}$

Damit ergibt sich für die Entropie jedes der ${\displaystyle N}$ Subsysteme die bekannte Formel

${\displaystyle \sigma =-\sum _{i=1}^{m}\omega _{i}\ln(\omega _{i})}$

In ähnlicher Weise erhält man (bis auf einen konstanten Vorfaktor) für den Informationsgehalt eines ebenso definierten Systems die Formel

${\displaystyle I=-\sum _{i=1}^{m}\omega _{i}\log _{2}{(\omega _{i})}}$

Siehe auch

• Gammafunktion

Einzelnachweise

1. ↑ G. Joos, Lehrbuch der theoretischen Physik 1956, S. 516

Literatur

• Eberhard Freitag, Rolf Busam: Funktionentheorie. 2. Aufl., Springer-Verlag, Berlin 1995.
• Konrad Königsberger: Analysis 1. Heidelberg, Springer 2003, ISBN 3-540-40371-X.

Weblinks

• Eric W. Weisstein: Stirling's Approximation. In: MathWorld (englisch).
• Pedro Sanchez, Aaron Krowne, Raymond Puzio u.a.: Stirling's approximation. In: PlanetMath. (englisch)
• Peter Luschny: Approximation Formulas for the Factorial Function Varianten und Alternativen zur Stirlingschen Formel (englisch).