Begegnungen eines Mathematikers mit Informatik #
von Ulrich Kulisch, angelehnt an seinen Vortrag anläßlich des 75sten Geburtstags im Juni 2008.Institut für Angewandte und Numerische Mathematik, Universität Karlsruhe, Karlsruher Institut für Technologie, D-76128 Karlsruhe, Germany.
Einführung#
Zur Orientierung möchte ich mit einer kurzen Bestandsaufnahme beginnen. In Deutschland findet jährlich eine Supercomputer-Tagung statt. Bei diesen Veranstaltungen werden die jeweils 500 schnellsten Rechner der Welt gelistet. Im Jahr 2008 war der schnellste Rechner ein Rechner von IBM für das Los Alamos National Laboratory in Neu Mexiko. Er soll dort für die Berechnung von Atomwaffen und die Simulation von Atombombenexplosionen eingesetzt werden. Er leistet knapp über ein Petaflops. Peta steht dabei für 1015 und Flops für Floating-point-operations per second, also Gleitkomma-Operationen pro Sekunde.Vor 20 Jahren war der schnellste Rechner die CRAY 2. Sie hatte erstmals die Gigaflops-Marke überschritten. Giga steht für 109. Von 2001 bis 2004 war der schnellste Rechner der japanische Erdsimulator in Yokohama. Er war in der Lage etwa 37 Teraflops auszuführen. Tera steht hier für 1012.
Mancher von Ihnen wird Schwierigkeiten haben, sich unter diesen großen Zahlen etwas Konkretes vorzustellen. Deswegen möchte ich einmal versuchen, diese etwas zu veranschaulichen. Wir fangen mal an mit dem Gigaflops-Computer. Ein guter PC leistet dies heute. Wir wollen versuchen, die Zahlen, die ein solcher Rechner in einer Sekunde produziert auf DIN-A4 Papier, also auf einem normalen Briefbogen auszudrucken. Wenn wir kleine Typen wählen, bekommen wir fünf Spalten und 100 Zeilen, also 500 Gleitkommazahlen auf eine Seite, wenn wir auf beide Seiten drucken, also 1000 Gleitkommazahlen auf ein Blatt. 1000 Blatt dünnes Papier ergeben einen Stapel von etwa 10 cm. 10 davon ergeben einen Meter.
Ein Gigaflops-Computer produziert also Zahlen in jeder Sekunde, die beidseitig auf DIN-A4-Papier ausgedruckt einen Stapel von 100 m ergeben würde. Das ist etwa doppelt so hoch wie der Karlsruher Schlossturm. Ein Teraflops-Computer ist 1000-mal schneller. Er produziert in jeder Sekunde einen Stapel von 100 km. Das ist etwa die Entfernung von Karlsruhe nach Darmstadt. Wenn ein solcher Rechner eine Stunde, also 3600 Sekunden rechnet, würde ein Stapel entstehen von 360 000 km. Das ist etwa die Entfernung von der Erde bis zum Mond. Der schnellste Rechner in unserem Rechenzentrum bringt im Jahr 2008 etwa eine Leistung von 16 Teraflops. Das wären in einer Stunde 16 Stapel von der Erde bis zum Mond.
Ein Petaflops-Computer ist noch einmal 1000-mal schneller als der Teraflops-Computer. Er würde in jeder Sekunde einen Stapel produzieren von 100 000 km, also 2 ½-mal um den Erdball. Wenn ein Rechner mit 25 Petaflops eine Minute rechnet entstünde ein Stapel von
Das ist in etwa die Entfernung von der Erde bis zur Sonne. Im Jahr 2017 gibt es bereits solche Rechner. Die Rechengeschwindigkeit ist also tatsächlich bereits in astronomische Größenordnungen vorgestoßen, s. Bild 1.
Rechengeschwindigkeit ist nicht alles#
Dabei muss man sich allerdings fragen, was hier eigentlich gemessen wird. Alle Rechner rechnen heute nach dem sog. IEEE Arithmetik Standard 754, der 1985 beschlossen wurde. IEEE steht dabei für Institute of Electrical and Electronics Engineers. Das ist bei uns vielleicht vergleichbar mit VDI/VDE. Gerechnet wird mit einem 64-bit-Wort, das entspricht etwa 16 Dezimalstellen.
Bild 2 und Bild 3 zeigen anhand einiger einfacher Beispiele aus einer Sammlung, die Herr Rump einmal zusammengestellt hat, was dabei passieren kann.
Im ersten Beispiel in Bild 2 werden fünf Zahlen addiert. Die einzelnen Zeilen unterscheiden sich nur dadurch, dass jedes Mal die Reihenfolge der Summanden vertauscht wird. Von den berechneten Ergebnissen ist nur 137 richtig. Alle anderen Ergebnisse sind falsch.
Im zweiten Beispiel wird die Lösung eines einfachen linearen Gleichungssystems mit zwei Unbekannten x und y berechnet. Die Formel für die Berechnung der Lösung und das korrekte Ergebnis sind angegeben. Das berechnete Ergebnis stimmt in keiner einzigen Stelle mit dem korrekten Ergebnis überein. Für die Berechnung von x und y sind jeweils nur vier arithmetische Operationen auszuführen.
Im dritten Beispiel wird das sog. Skalarprodukt zweier Vektoren mit jeweils fünf Komponenten berechnet. Die Formel und das korrekte Ergebnis sind angegeben. Das mit dem Computer berechnete Ergebnis stimmt wieder in keiner einzigen Stelle mit dem korrekten Ergebnis überein. Sogar das Vorzeichen ist falsch. In diesem Beispiel sind insgesamt neun arithmetische Operationen auszuführen. Keines der Daten in den drei Beispielen hat mehr als 10 Ziffern. Die Rechnung erfolgt mit jeweils etwa 16 dezimalen Ziffern.
Das Beispiel in Bild 3 zeigt, dass auch der Übergang zu höherer Genauigkeit kein Allheilmittel darstellt. Eine einfache Formel wird für zwei Werte ausgewertet mit umgerechnet 8, 16 und 32 dezimalen Ziffern. Der Rechner liefert in allen Fällen das gleiche Ergebnis. Dieses stimmt in keiner einzigen Stelle und auch nicht im Vorzeichen mit dem korrekten Ergebnis überein.
Mit den hier gezeigten Algorithmen bzw. Formeln kann man für andere Daten durchaus die korrekten Ergebnisse ausrechnen. Es sind die speziellen Datenkonstellationen, welche die Rechnung zum Absturz bringen. Wer kann aber schon übersehen, was für Datenkonstellationen bei einer Rechnung auftreten, welche 109, 1012 oder sogar 1015 Operationen in der Sekunde ausführt. Mit anderen Worten: Die hohen Rechengeschwindigkeiten stellen das Rechnen mit einfachen Gleitkommazahlen, wie es heute auf allen kommerziell verfügbaren Rechnern zur Verfügung steht, selbst in Frage.
Die gezeigten Ergebnisse erhält man auf allen Rechnern, die man heute kaufen kann. Viele Leute und sogar solche, die es eigentlich besser wissen sollten, glauben daher, dass dies so sein muss. Das ist ein ganz schrecklicher Aberglaube. Ein Computerchip enthält heute einige Milliarden Transistoren. Man könnte Rechner auch so bauen, dass solche Fehler nicht mehr auftreten.
Es ist eigentlich nicht mehr sinnvoll zu fragen, wie schnell ein Rechner gewisse einfache Operationen ausführen kann. Wenn man stattdessen fragen würde: Wie schnell kann man bei gewissen Aufgaben fünf, zehn oder fünfzehn korrekte Stellen berechnen, würde dies sehr schnell zu wesentlich besseren und geeigneteren Rechnern führen.
Mehr Vorsicht ist angebracht#
Ganz besonders vorsichtig und sorgfältig müsste man natürlich vorgehen, wenn Rechner zur Berechnung von Atomwaffen oder der Simulation von Atombomben eingesetzt werden. Hierzu läuft in den USA das sog. ASCI-Programm. Es wird vom US-Department of Energy mit jeweils 200 Millionen Dollar jährlich in amerikanischen Großforschungseinrichtungen betrieben. ASCI steht für Advanced Strategic Computing Initiative. „It aims to replace physical nuclear weapons testing with computer simulations”.
Hierzu gibt es einen kritischen Bericht von John Gustafson vom US-Department of Energy zum Thema: Computational Verifyability and Feasibility of the ASCI Program. Der Autor erläutert darin, dass die Fehleranfälligkeit und blindes Vertrauen in herkömmliche Berechnungen zu einem Nuclear Disaster führen kann. Die USA haben das Atomwaffenteststopabkommen unterschrieben. Die Weiterentwicklung von Atomwaffen kann daher nur mittels Berechnungen erfolgen. Er schreibt dann: This forces us to a very different style of computing, one with which very few people have much experience, where results must come with guarantees. This is a new kind of science ....
Eine einzige falsche Operation kann eine ganze Rechnung wertlos machen. Später in seinem Bericht heißt es dann wörtlich: “Germany, specifically the University of Karlsruhe, remains the centre of activity on interval arithmetic and verifiable numerical computing, .... We would do well in the ASCI-program to echo the fervor of the Germans for numerical verifiability.”
Ich hoffe, dass die Universität Karlsruhe in der Lage ist, sich diesen Ruf zu erhalten.
Seit etwa 2002 wird an einer Revision des sog. IEEE Arithmetik Standards gearbeitet. Dazu trifft sich praktisch monatlich eine Gruppe von etwa 100 Wissenschaftlern abwechselnd bei Firmen in der Gegend zwischen San Francisco und San José. Die Besprechungsprotokolle konnte man im Internet verfolgen. Ich habe während der letzten Jahre mit einer Anzahl von Briefen versucht, die Entwicklung eines Nachfolgestandards dahingehend zu beeinflussen, dass die Rechner so weiterentwickelt werden, dass sie selbst zur Kontrolle von Rechenergebnissen eingesetzt werden können. Ein Teil meiner Briefe kann auf meiner Homepage an der Universität Karlsruhe eingesehen werden. Der GAMM-Fachausschuss Rechnerarithmetik und Wissenschaftliches Rechnen hat den Inhalt meiner Briefe im Jahre 2006 durch eine eigene Eingabe unterstützt. Auch ein Fachausschuss der IFIP (IFIP steht für International Federation for Information Processing. Es ist so etwas wie eine Dachorganisation aller Computer Science Gesellschaften.) hat sich mit einem eigenen Schreiben an das IEEE-Standardkomitee gewandt, Bild 4 und Bild 5.
Intervallarithmetik#
Darin werden zwei zentrale Forderungen a) und b) erhoben. Ohne hier näher auf Details einzugehen, möchte ich nur erwähnen, dass zu der Forderung a) eine Arbeit von Herrn Kirchner und mir zitiert wird und zu der Forderung b) ein Buch von mir, das ich nach meiner Emeritierung während mehrerer Forschungsaufenthalte in Japan geschrieben habe.
Die Antwort auf diese Eingaben sagte, dass das IEEE-Computerarithmetik-Revisionskomitee diese Vorschläge wiederholt intensiv diskutiert hat, dass aber das Gefühl vorherrscht, nicht das nötig Know-how zu besitzen, um hier eindeutige Vorgaben machen zu können. Am 12. Juni 2008 hat daraufhin die IEEE-Computer Society ein Standardkomitee IEEE-P1788 für Intervallarithmetik gegründet, welches die arithmetischen Eigenschaften festlegen soll, welche benötigt werden, um mit dem Rechner selbst Rechenergebnisse garantieren zu können.
Persönliche Erlebnisse#
Ich möchte nun etwas genauer auf mein eigentliches Thema: Begegnungen eines Mathematikers mit Informatik zu sprechen kommen. Durch glückliche Umstände bin ich recht früh mit diesen Dingen in Berührung gekommen. Im Jahre 1953 habe ich in München ein Studium der Mathematik und Physik begonnen. Im Herbst 1954 kündigte Prof. Heinhold ein Proseminar über Rechenmaschinen an. Das Institut für Angewandte Mathematik an der TH München verfügte über eine große Palette analoger und digitaler mechanischer Rechenmaschinen, Integraphen, Integrimeter, Planimeter, Fourieranalysatoren, Stieltjesintegratoren und alle Arten mechanischer digitaler Rechenmaschinen. Mir wurde die Aufgabe zugewiesen, die verschiedenen Arten digitaler Rechenmaschinen, Staffelwalzen-, Sprossenrad-, Schaltklinken-, Proportionalhebel-maschinen und andere, zu erklären und typische Rechenbeispiele damit vorzuführen.Dies war für mich damals eine völlig neue Erkenntnis. Rechnen war für mich bis dahin eine geistige Tätigkeit. In der Schule hatten wir mit der Logarithmentafel gerechnet und im physikalischen Praktikum mit dem Rechenschieber oder von Hand. Jetzt erkannte ich, dass man das Rechnen auch mit Maschinen, und zwar sogar mittels relativ einfacher und einsichtiger Prinzipien, ausführen kann. Dies hat mich derart fasziniert, dass ich jede freie Minute genutzt habe, um in die Bibliothek des Deutschen Museums zu fahren und alles nachzulesen, was man über historische Rechengeräte finden konnte.
Die Bilder 6, 7 und 8 zeigen drei alte mechanische Digitalrechner, eine Sprossenradmaschine Trinks-Brunsviga aus Braunschweig aus dem Jahre 1917, eine Maschine MADAS (steht für Multiplikation, Automatische Division, Addition und Subtraktion) der Schweizer Firma Egli aus dem Jahre 1936 und eine amerikanische Maschine Monromatik aus dem Jahre 1956. Die beiden letzten Maschinen haben ganz oben noch ein Akumulationsregister, in das man Zahlen und einfache Produkte von Zahlen in Festkommaarithmetik fehlerfrei akkumulieren konnte. Würde man diese alte, äußerst wirksame und nützliche Operation auch bei heutigen elektronischen Digitalrechnern realisieren, so ließen sich sehr viele der heute auftretenden Rechenfehler vermeiden.
Am Ende des Semesters wurde der Hörsaal, in dem ich meinen Vortrag gehalten hatte, geschlossen und man erfuhr, dass hier ein Zwischengeschoss eingezogen wird, und dass dort eine große elektronische digitale Rechenanlage aufgebaut werden soll. Die DFG hatte für ein Gemeinschaftsprojekt von Prof. Robert Sauer, Mathematik und Prof. Hans Piloty, Elektrotechnik eine Million DM bewilligt.
Im Sommersemester 1956 boten Prof. Sauer und Dr. Bauer, der sich damals gerade habilitiert hatte, ein Seminar über die PERM an. PERM steht für Programmgesteuerter Elektronischer Rechenautomat München, Bild 9. Ich ging wieder in dieses Seminar. Wir waren damals nur drei Studenten, die sich dafür interessierten. Alle anderen Teilnehmer waren Mitarbeiter aus verschiedenen Instituten oder aus der Industrie. Ich bekam als Vortrag das Thema Die Kodierung der PERM. Die Entwickler der Anlage waren damals sehr stolz; denn Herr Schecher hatte gerade einen Compiler implementiert.

Der Compiler übersetzte den symbolischen Code in den Interncode der Anlage. Meine Aufgabe bestand also darin, den symbolischen Code zu erläutern und einfache Programmbeispiele damit vorzuführen. Über die generelle Situation elektronischer Rechner konnte man sich damals recht gut informieren. Die Schweizer Mathematiker Rutishauser, Speiser und Stiefel hatten in der ZAMP (Zeitschrift für Angewandte Mathematik und Physik) bereits Anfang der 1950er Jahre drei einführende Artikel, damals sogar noch auf Deutsch, veröffentlicht. Sie hatten ja bereits 1948/49 die Z4 von Zuse erworben, konnten also bereits rechnen und waren hoch motiviert. Sie hatten als Schweizer auch Zugang zu allen in den USA damals laufenden Entwicklungen.
Am Ende des Semesters gab mir Prof. Heinhold gleich ein Thema für meine Examensarbeit. Ich sollte ein Verfahren und ein zugehöriges Programm entwickeln, welches den Einheitskreis konform auf ein sternförmiges Gebiet abbildet. Ich habe mir damals ein Verfahren ausgedacht, welches mit Fourierreihen arbeitet. Da brauchte ich natürlich die elementaren Funktionen, welche noch gar nicht verfügbar waren. Herr Dr. Samelson, der damals noch Assistent bei Prof. Sauer war, hat sie dann kurzfristig für mich implementiert.
Als ich mein Verfahren programmiert hatte, gab ich meinen Lochstreifen bei der PERM-Mannschaft ab. In der Folgezeit schaute ich immer wieder mal dort vorbei in der Hoffnung, dass mein Programm inzwischen ausgeführt wurde. Jedes Mal ermahnte mich Herr Samelson: „Schauen Sie Ihr Programm gut an, Sie bekommen nur einen einzigen Lauf.“ Was soll diese ständige Ermahnung, dachte ich mir. Ich hätte ihm mein Programm, einige hundert Zeilen Code, auswendig vorbeten können. Endlich war es dann so weit. An einem Abend wurde mein Programm als Letztes eingegeben. Am nächsten Morgen sollte die PERM umgebaut und eine Kernspeichererweiterung eingebaut werden. Als ich meine Ergebnisse ansah, stellte ich fest, dass es nicht iteriert hatte. Ich hatte zwei Befehle in der falschen Reihenfolge aufgeschrieben. Schnell habe ich meinen Lochstreifen korrigiert und am nächsten Morgen um 6 Uhr saß ich vor der Tür zur PERM. Irgendwann, dachte ich, wird Herr Dr. Annacker, der damals für den Betrieb zuständig war, kommen, dann werde ich ihn bitten, den Rechner noch einmal einzuschalten und mein Programm noch einmal laufen zu lassen. Gegen 8 Uhr kam Herr Annacker, tat, worum ich ihn gebeten hatte, und diesmal hatte es iteriert. Ich hatte meine Ergebnisse und konnte mich zum Examen anmelden.
15 Jahre später verbrachte ich ein Forschungssemester am IBM-Forschungszentrum in Yorktown Heights, N.Y., USA. Herr Annacker war hier inzwischen zu einem hochrangigen Manager bei IBM aufgestiegen. Er war der verantwortliche Leiter für die Entwicklung eines superschnellen Rechners, der Prinzipien der Supraleitung ausnutzte.
Die Entwicklung ging dann rasch weiter. Herr Seegmüller hat für die PERM einen der ersten ALGOL-Compiler überhaupt geschrieben. Von 1964 bis 1966 habe ich einen Lehrstuhl für numerische Mathematik an der Universität München vertreten. Die Übungen dazu haben wir damals mit mehreren hundert Studenten bereits in ALGOL immer noch auf der PERM ausgeführt.
Mehr als eine Entwicklung#
Die PERM war nicht die einzige Maschine, welche damals an Hochschulen und Forschungszentren entwickelt wurde, Bild 10. Am Max-Planck-Institut in Göttingen entstanden gleich drei Anlagen unter Herrn Dr. Billing, Bild 11. Auf der G2 hat Herr Martensen damals noch gerechnet. Eine weitere Anlage wurde bei Prof. Walther in Darmstadt entwickelt, Bild 12. Herr Görke hat mir einmal erzählt, dass die Darmstädter Anlage nie richtig in der Produktion gelaufen ist. Bei Herrn Prof. Lehmann in Dresden entstanden gleich mehrere Rechner, die z.T. auch erfolgreich vermarktet wurden. Ein anderer Rechner wurde von Herrn Prof. Kämmerer bei Zeis in Jena entwickelt. Einige kleinere Anlagen entstanden auch in Zürich und bei Prof. Zemanek in Wien.
Der Funke ist dann tatsächlich auch auf die Industrie übergesprungen und es kam zu kommerziellen Entwicklungen bei SIEMENS, Telefunken, SEL (Standard Electric Lorenz) und bei der Zuse KG, Bild 13. Auch in anderen europäischen Ländern kam es damals zu zahlreichen Entwicklungen kommerzieller Rechner. Es herrschte eine Art Aufbruchstimmung. Überall wollte man dabei sein.
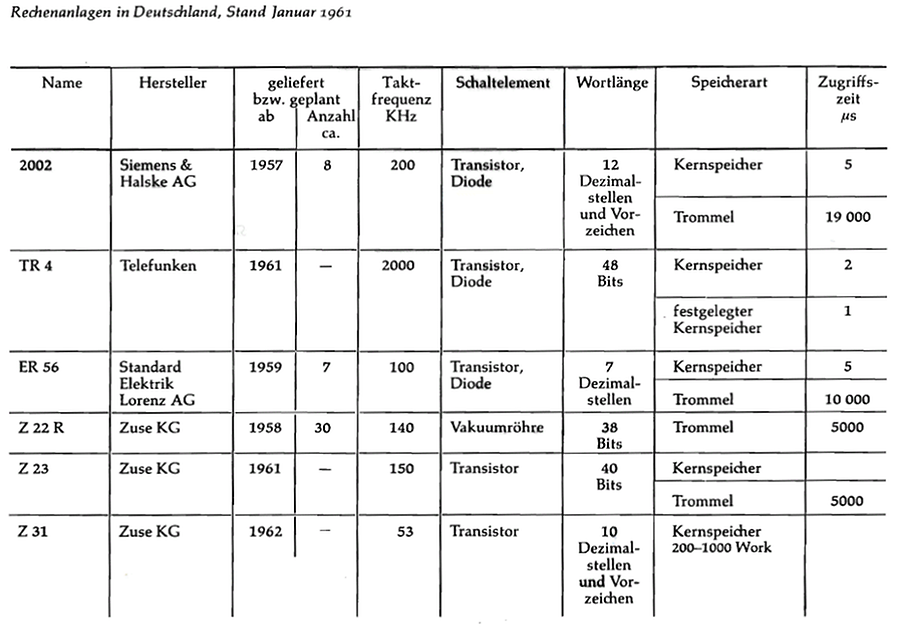
In dem Buch: Rechnen mit Maschinen von W.G. Bauclair (1968) werden bis zum Jahre 1962 allein für England etwa 20 kommerzielle Rechnerenwicklungen gelistet, für Frankreich 7. Aber auch in Holland, Italien, Schweden, Dänemark und der Tschechoslowakei kam es zur Entwicklung kommerzieller Rechenanlagen.
Wenn man dies alles miterlebt hat, stimmt es einen irgendwie traurig, dass man heute feststellen muss, dass von all dem nichts mehr übrig geblieben ist. Als wir in Deutschland die Informatik angeschoben haben, gehörte ich allen einschlägigen Bonner Ausschüssen (Einführung von Informatikstudiengängen, Überregionales Forschungsprogramm Informatik) übrigens als einziger Professor aus Karlsruhe an. Von einer einschlägigen Sitzung im Forschungsministerium habe ich einmal die Unterschriftenliste anwesender Kollegen kopiert, welche sich damals für die Gründung einer Gesellschaft für Informatik eingesetzt haben, Bild 14. Darin habe ich diejenigen Mitglieder mit einem Punkt gekennzeichnet, welche damals der Kommission für Rechenanlagen der deutschen Forschungsgemeinschaft angehörten. Ich war damals ebenfalls Mitglied dieser Kommission. Beim Aufbau der Informatik war dies die eigentlich treibende Gruppe. Von diesen zehn Mitgliedern habe ich diejenigen Namen mit einem zweiten Punkt gekennzeichnet, welche einmal aktiv am Bau von Rechenanlagen beteiligt waren. Das sind sechs von zehn Mitgliedern der Kommission für Rechenanlagen. Zumindest bei diesen und mich kann man hier ohne weiteres hinzuzählen, schwang damals die Hoffnung mit, dass ein Anschub der Informatik in Deutschland auch die Rechenmaschinenindustrie in unserem Lande voranbringen würde. Dies ist leider nicht eingetreten.
Ein amerikanischer Kollege hat mir einmal einen etwa 300 Seiten starken Bericht mit dem Titel: Getting up to Speed, The Future of Supercomputing, des National Research Councel of the National Academies der USA zugespielt, Bild 15. Darin kann man nachlesen, was amerikanische Kollegen ihrem Präsidenten vorschlagen, was auf dem Gebiete des Computers in den nächsten Jahren geforscht und entwickelt werden soll. Ein sehr häufiges Wort in diesem Bericht ist Leadership. Der Bericht bringt den unbedingten Willen zum Ausdruck, auf dem Gebiete der Computerentwicklung über Jahrzehnte hinweg in der Welt eine führende Stellung einzunehmen. Die 500 Millionen Europäer werden als willkommene Käufer gesehen, die man immer mal wieder anspornen muss, tüchtig zu rechnen.
Vier Epsisoden#
Den Rest des mir noch zur Verfügung stehenden Platzes, möchte ich dazu verwenden, Ihnen an vier Episoden, die sich alle während meiner aktiven Zeit in Karlsruhe zugetragen haben, vorzuführen, dass man sich schwerwiegende Nachteile einhandelt und immer wieder teures Lehrgeld dafür bezahlen muss, dass es in Europa keine eigenständige Rechnerentwicklung mehr gibt.
Am 1. April 1966 habe ich meinen Dienst an der Universität Karlsruhe angetreten. Zu meinen Pflichten gehörte es damals, ein Rechenzentrum aufzubauen und zu leiten. Im Vergleich mit anderen technischen Hochschulen war die Technische Hochschule Karlsruhe bei der Rechenmaschinenausstattung damals ohne Zweifel rückständig. Es gab nur zwei kleine Zuse-Anlagen in der Angewandten Mathematik und einen ER56 von SEL am Institut von Prof. Steinbuch. Alle Anlagen waren ohne ein Betriebssystem geliefert worden. Die Herren Dr. Wettstein und Berger hatten aber für den ER56 bereits ein einfaches Betriebssystem entwickelt. Damit lief diese Anlage relativ zuverlässig. Eine weitere Anlage EL X8 von der holländischen Firma Elektrologica war bereits bestellt. Auf meine Frage, ob die X8 über ein Betriebssystem verfügt, lautete die Antwort nein. Dies war eine sehr schwierige Situation.
Am MIT war damals aber ein Multiuser-Betriebssystem, das MAC-System, in Entwicklung. Da hatte Prof. Nickel die Idee, so etwas machen wir auch. Wir entwickeln für die X8 ein Hydra-Betriebssystem, einen Rechner mit mehreren Benutzerterminals. Dies konnte man der DFG als Forschungsvorhaben verkaufen. Die DFG bewilligte großzügig die Mittel. Offenbar hatte man dort selbst ein schlechtes Gewissen, denn die DFG hatte drei solcher Anlagen gekauft, die beiden anderen für die Universitäten Würzburg und Kiel.
Prof. Nickel heuerte daraufhin die Herren Dr. Wettstein und Dr. Brockhaus aus dem Bereich Steinbuch an. Sie sollten ein Multiuser-Betriebssystem für die X8 entwickeln. Herr Berger aus dem Bereich Steinbuch kam ohnehin ans Rechenzentrum. Im Oktober/November 1966 wurde die X8 ausgeliefert und im Keller des Mathematikgebäudes aufgestellt.
Ende 1969 hat Herr Wettstein das Hydra-Betriebssystem für die X8 zur allgemeinen Benutzung freigegeben, Das System arbeitete sehr überzeugend. Man hätte damals bis zu 32 Fernschreiber an die X8 anschließen können. An jedem Fernschreiber konnte ein Benutzer sein Programm erstellen, übersetzen, Fehler korrigieren und rechnen lassen. Die Ergebnisse wurden am selben Fernschreiber ausgegeben. Jeder Benutzer hatte also den Eindruck, einen eigenen Rechner zu besitzen.
Ich habe damals die Firma Elektrologica aufgesucht und vorgeschlagen, die X8 in neuer Technologie noch einmal herauszubringen und mit dem Wettstein’schen Betriebssystem zu vermarkten. Es wäre ein wunderbarer Ausbildungsrechner gewesen. Man zeigte sich durchaus an dem Vorschlag interessiert. Bald danach wurde Elektrologica aber von Philips aufgekauft, und die hatten ganz andere Pläne.
Tatsache ist, dass sich damals kein einziges Institut der Universität Karlsruhe mehr mittels eines Fernschreibers an die X8 angeschlossen hat. Ein Anschluss hätte das Institut 27 000 DM für einen Fernschreiber und Anschlusselektronik gekostet und dazu vier Telefonleitungen. Die Universität hatte damals keine freien Telefonleitungen zu vergeben. Ein wesentlicher Grund aber war der, dass wir nach einem intensiven Auswahlverfahren, an dem sich zahlreiche Institute der Universität beteiligt hatten, bereits ein halbes Jahr vorher eine Nachfolgerechenanlage, eine Dreiprozessoranlage, UNIVAC 1108, für 23 Millionen DM für das Rechenzentrum beantragt hatten, zudem ein neues Gebäude mit einem Anbau für die Informatik. Tatsächlich wurde die UNIVAC 1108 auch bereits ein Jahr später ausgeliefert.
Das wunderbare Wettstein’sche Betriebssystem Hydra konnte fortan nur noch von einigen Fernschreibern in einem Nebenraum zur X8 im Rechenzentrum benutzt werden.
11 Jahre später brachte IBM den PC auf den Markt mit einem Betriebssystem, das bei weitem nicht die Qualitäten des Wettstein’schen Betriebssystems besaß. Die Leute, die damals das Betriebssystem für den PC entwickelt hatten, haben sich goldene Nasen verdient und haben heute viele Milliarden Dollar auf dem Konto. Wir haben damals erstmals die bittere Erfahrung gemacht, dass man, wenn man prozessornahe Software entwickelt für einen Prozessor, der bereits auf dem Markt ist, mit der Software auf dem Markt keinen Erfolg haben kann; denn drei Jahre später gilt der Prozessor als veraltet und niemand interessiert sich mehr, auch nicht für die allerbeste Software.
Ich komme nun zu meiner zweiten Episode, die ich hier schildern möchte. Im Jahre 1975 erhielt ich einen Ruf auf den ersten Lehrstuhl für Informatik an der Universität Paderborn. Paderborn war die Stadt der Firma Nixdorf. Sie hatte gerade die Marke von einer Milliarde Umsatz pro Jahr überschritten. Ich hatte gerade ein kleines Buch veröffentlicht mit dem Titel: Grundlagen des Numerischen Rechnens - Mathematische Begründung der Rechenarithmetik, Bild 17.
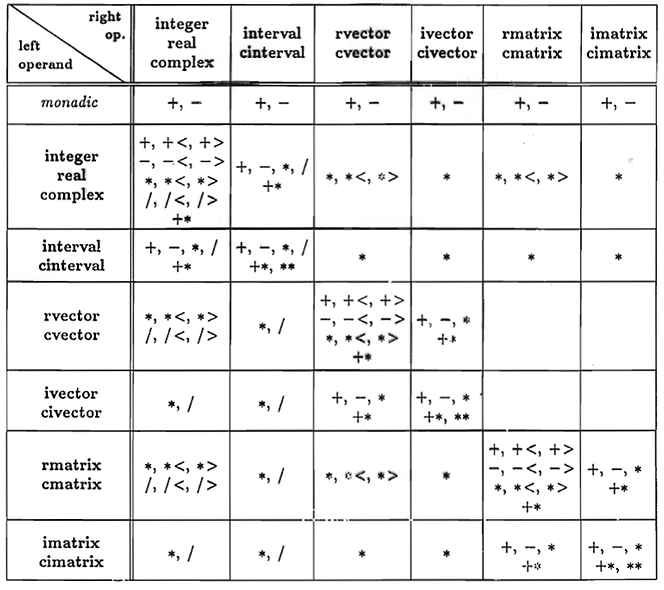
Darin wird vorgeschlagen, zur Vermeidung unnötiger Rundungsfehler nicht nur die vier Grundrechenoperationen für Gleitkommazahlen, sondern darüber hinaus auch noch Verknüpfungen in höheren mathematischen Räumen, wie komplexe Zahlen, Vektoren, Matrizen und Intervallen darüber, usw. im Rechner mit maximaler Genauigkeit direkt zur Verfügung zu stellen, an Stelle sie über die übliche Gleitkommaarithmetik zum Teil fehlerhaft zu approximieren, Bild 18.
Mit diesem Buch in der Hand besuchte ich die Firma Nixdorf und schlug vor im Falle meines Wechselns an die Universität Paderborn einmal gemeinsam einen Rechner aufzubauen, der nach diesen Prinzipien arbeitet. Herr Nixdorf ging auf diesen Vorschlag ein. Der Bund zahlte auch noch etwas dazu, und so hatten wir ein Projekt von der Größenordnung 1 Million DM. Der neue Rechner sollte auf einem Mikroprozessor Z80 rein softwaremäßig realisiert werden. Es gab damals keine Programmiersprache, mit der man die vielen arithmetischen Operatoren durch einfache Operationszeichen hätte ansprechen können. Es war aber gerade die Sprache PASCAL aufgekommen. Wir erweiterten also die Sprache durch ein allgemeines Operatorkonzept und andere Konstrukte, die wir brauchten. Für die neue Sprache musste nun ein neuer Compiler entwickelt werden.
Anfang 1980 lief das ganze System. Wir gaben ihm den Namen PASCAL-XSC (PASCAL for Extended Scientific Computing), Bild 19.Hier kam uns der Umstand entgegen, dass Herr Prof. Wippermann, der sich hier am Rechenzentrum einmal habilitiert hatte und nach einer dreijährigen Professur in Berlin inzwischen Professur für Informatik an der Universität Kaiserslautern war mit dem Schwerpunkt Compilerbau.
Wir gaben damals drei Mitarbeiter nach Kaiserslautern ab, welche dort unter der Regie von Herr Wippermann den Compiler entwickelten. Einer davon war Herr Neaga, welcher heute die musikalische Umrahmung gestaltet. Ein zweiter war Herr Kirchner, welcher heute noch eine Säule der Informatik in Kaiserslautern ist. Der dritte war Herr Allendörfer. Er hat später noch mit Kollegen von der ETH Zürich ein zu unserem PASCAL-XSC entsprechendes Oberon-XSC entwickelt. Herr Bohlender und Herr Grüner implementierten in Karlsruhe die vielen (einige hundert) arithmetischen Operatoren, alle mit maximaler Genauigkeit, und Herr Wolff von Gudenberg implementierte die Standardfunktionen. Eine andere Gruppe bestehend aus den Herren Kaucher, Rump und Böhm implementierte für eine große Anzahl von Grundaufgaben der Numerik Routinen, bei denen der Rechner stets enge Schranken für die gesuchte Lösung berechnet.
Anfang 1980 lief das ganze System. Wir gaben ihm den Namen PASCAL-XSC (PASCAL for Extended Scientific Computing), Bild 19.
Wir haben es dann im April 1980 auf der Hannovermesse auf einem Stand der Firma Nixdorf ausgestellt. Herr Kirchner und ich haben es dort vorgeführt.
Der ganze Vorstand der Firma Nixdorf kam vorbei und war von unserem neuen Rechner begeistert. Vier Wochen später sollten wir nach Paderborn kommen, um über eine Vermarktung zu sprechen. Eine Woche vor Ablauf dieser Frist bekam ich einen Anruf, in dem mir mitgeteilt wurde, dass man beschlossen habe, das System nicht zu vermarkten.
Herr Luft, der damalige Vertriebschef der Firma Nixdorf, war der Meinung, dass der Prozessor inzwischen veraltet sei und dass man einen Rechner, der für ca. 12 000 DM kalkuliert war, nicht profitabel verkaufen kann.
Rechner wurden damals durch mehrmaligen Besuch und Überzeugungsarbeit beim Kunden vermarktet. Eineinhalb Jahre später kam IBM mit dem PC auf den Markt. Er wurde von Anfang an über den üblichen Elektrofachhandel vertrieben.
Herr Nixdorf war aber nicht kleinlich. Er stellte uns einige solcher Systeme samt Tischen und Stühlen zur Verfügung.

Damit konnten wir schon im Sommersemester 1980 einen Teil der Programmierausbildung an der Universität Karlsruhe dezentralisieren, Bild 20. Herr Krämer hat den Praktikumsbetrieb damals eingerichtet. Herrn Nixdorf wurde daraufhin die Würde eines Ehrensenators an der Universität Karlsruhe verliehen.
Unsere Sprachbeschreibung PASCAL-XSC ist auf deutsch, englisch und russisch erschienen, Bild 21, 22. Auch ein zugehöriger Toolboxband mit Problemlöseroutinen, mit automatischer Ergebnisverifikation ist ins Russische übersetzt worden und 2006 erschienen, Bild 23. Die russische Übersetzung unserer Sprachbeschreibung ist inzwischen in dritter Auflage erschienen, Bild 24.

Die Sprache wird immer noch benutzt. Einen entsprechenden Compiler stellt das Institut von Herrn Krämer, der inzwischen Professor an der Universität Wuppertal ist, kostenlos zur Verfügung. Wieder hatten wir prozessornahe, sehr fortschrittliche Software entwickelt, für einen Prozessor, der bereits auf dem Markt war. Als das endgültige Produkt vorlag, galt der Prozessor als veraltet.
Die Fähigkeiten unseres neuen Rechners, Rechenergebnisse garantieren zu können, sprachen sich rasch herum. Professor Ganzhorn, damals oberster Chef von IBM in Europa, bat um eine Vorführung. Nach einer Viertelstunde war er überzeugt und sagte: „Das kommt in jeden IBM-Rechner.“ Er stellte uns einen Betreuer, Herrn Dr. H. Bleher, zur Verfügung.
Ich freue mich, Herr Dr. Bleher, dass Sie heute auch nach Karlsruhe gekommen sind. Wir sprachen dann Schritt für Schritt ab, was der Reihe nach realisiert werden sollte. Ein erstes Produkt war 1983 fertig, Bild 25.
Es handelt sich dabei um eine Unterprogrammbibliothek für Grundaufgaben der Numerik, wie lineare Gleichungssysteme, Eigenwertprobleme, Optimierungsprobleme, Nullstellenberechnungen, usw., bei denen der Rechner stets enge Schranken für die gesuchte Lösung berechnet. Wir haben unser Produkt auch gleich auf einer Informationsveranstaltung im NTI-Hörsaal der Universität Karlsruhe bekannt gemacht. Am Ende der Veranstaltung kam Herr Wettstein, der inzwischen Professor für Informatik in Karlsruhe war, zu mir und sagte: „Herr Kulisch, ich gratuliere Ihnen, sie haben Ihre Ideen beim Marktführer und damit endgültig im Markt etabliert.“ Das glaubten damals viele. Fast alle namhaften Rechnerhersteller bauten damals die IBM/370-Architektur: Amdahl, Philips, Siemens, Hitachi, NEC, Fijutsu, u.a.
Damit wir unsere Arithmetik einfach realisieren konnten, hatte IBM uns auf Anlagen der /370-Architektur 20 neue Befehle zur Verfügung gestellt. Nach nur wenigen Wochen hat auch die japanische Firma Hitachi diese Befehle auf ihren Anlagen angeboten. Die Firma Siemens, welche damals ebenfalls Anlagen der /370-Architektur entwickelte hat unser ganzes Produkt, welches den Namen ACRITH erhalten hatte, auf eigenen Anlagen nach entwickelt und unter dem Namen ARITHMOS vertrieben. Trotz dieser Anfangserfolge sollte Herr Wettstein langfristig nicht Recht behalten.
Unser langfristiges Ziel war natürlich die Entwicklung einer Fortran-Erweiterung in Analogie zu unserem PASCAL-XSC, welche es dem Benutzer ermöglichen sollte, selbst Programme mit automatischer Ergebnisgarantie zu entwickeln.
Da mussten wir zunächst wieder die Sprache Fortran erweitern, damit die vielen zusätzlichen arithmetischen Operatoren einfach angesprochen werden können. Dies machte einen neuen Compiler erforderlich. Den mussten wir diesmal selbst entwickeln. Dazu haben wir damals Herrn Wolfgang V. Walter angeheuert. Er hatte in der Schweiz studiert und war dort schon einige Zeit mit Compilerbauarbeiten für Niklaus Wirth betraut. Wir stellten ihm einige unserer Absolventen, die Herren Metzger, Schmidt, Davidenkoff u.a. zur Seite.
Als besonders schwieriges Problem entpuppte sich damals die Implementierung der Standardfunktionen. Wenn man eine Sprache entwickelt, welche es dem Benutzer ermöglichen soll, Rechenergebnisse zu garantieren, müssen auch die Standardfunktionen mit garantierten Schranken berechnet werden. So etwas gab es damals nicht. Wenn man auf damals üblichen Prozessoren etwa den Kosinus aufrief, bekam man zwar 16 Stellen ausgedruckt, davon waren aber u.U. nur fünf Stellen richtig. Der Benutzer wusste ja nicht, wie es dahinter weitergeht. Wenn man hingegen Schranken abliefern muss, sieht der Benutzer sofort, wie genau die Funktion berechnet wurde.
IBM verlangte höchste Genauigkeit für 24 Funktionen für die vier Datentypen real, complex, interval und complex-interval für die beiden Datenformate short und long. Dies war eine riesige Aufgabe. Ein komplexes Intervall ist beispielsweise ein achsenparalleles Rechteck in der komplexen Zahlenebene. Es mussten hochgenaue Schranken in solchen Bereichen geliefert werden. Unter den in Frage kommenden Funktionen befinden sich auch mehrwertige Funktionen. Es muss dann jeweils entschieden werden, wie der Schnitt auf der zugehörigen Riemannschen Fläche zu wählen ist.
Herr Krämer und Herr Braune haben diese Arbeiten damals bravourös bewältigt. Die von den Herren Krämer und Braune damals bereitgestellten Funktionen hatten großen Einfluss auf die Standardfunktionen bei allen anderen Prozessoren. Es lagen ja jetzt Referenzfunktionen vor, mit denen man die Funktionen eines gegebenen Prozessors vergleichen konnte. Die Qualität der Standardfunktionen hat sich seither auf allen Prozessoren ganz wesentlich verbessert.
Ende 1989 war unsere Spracherweiterung fertig und wurde von IBM unter dem Namen ACRITH-XSC als IBM Program Product auf den Markt gebracht, Bild 26.
Der Absatz war zunächst zufriedenstellend. Er brach aber nach geraumer Zeit plötzlich ein.
Was war passiert? In den 1980er Jahren sind viele neue Architekturen auf den Markt gekommen.
1981/82 kam der PC, 1983/84 die Workstations, dazu gehört auch die RS6000 Power Architektur von IBM und 1984/85 kamen auch die ersten Supercomputer auf den Markt.
Das wissenschaftliche Rechnen ist während der 1980er Jahre von den alten Großrechnern der /370-Architektur weggewandert auf diese neuen Architekturen, die vielfach unter UNIX-Betriebssystemen angeboten wurden. Als wir unsere Arbeiten im Jahre 1980 begannen, gab es bei IBM nur die /370-Architektur.
Als wir fertig waren, galt diese im Bereich des wissenschaftlichen Rechnens als veraltet. Wieder waren wir mit einem zukunftsweisenden Produkt auf der Prozessorseite abgehängt worden.
Wir sind dann noch mit fünf Mann zu IBM nach Austin/Texas gereist zu einer Besprechung darüber, was zu tun sei, um unser Produkt auf die neue IBM Power Architektur zu übertragen. Es wurde vereinbart, dass ich einschlägige Literatur und eine Anleitung dorthin schicke, wie bei einer Übertragung zweckmäßigerweise vorgegangen werden soll.
Nach etwa drei Wochen habe ich ein großes Paket von Karlsruhe nach Austin abgeschickt. Nach weiteren drei Wochen kam es zurück mit der Bemerkung, die Empfänger seien nicht mehr bei IBM.
IBM war damals im Begriff sein Personal um 50 % zu reduzieren. In dieser Phase wurden alle möglichen Abfindungsprogramme herausgebracht mit dem Ergebnis, dass gerade kompetente Mitarbeiter sich kurzfristig entschlossen auszuscheiden und bei anderen Firmen unterzukommen. So sind uns wichtige Ansprechpartner bei IBM damals verloren gegangen.
Ich komme nun zu meiner vierten und letzten Episode, die ich hier ansprechen möchte. Im Jahre 1985 erhielt ich einen Ruf an das Hahn-Meitner-Institut in Berlin. Es handelte sich um einen Lehrstuhl für Mathematik an der Freien Universität und um ein großes Institut für Informatik am Hahn-Meitner-Institut. In Erhaltungsverhandlungen wurde meinem Institut in Karlsruhe ein nicht unerheblicher jährlicher Forschungsetat in Aussicht gestellt. Aus politischen Gründen entschloss ich mich damals, den Ruf nach Berlin nicht anzunehmen. Nachdem wir mit durchaus zukunftsweisenden Softwareentwicklungen bereits mehrmals auf der Prozessorseite ins Abseits geraten waren, lag die Versuchung nahe, es einmal selbst mit einer Hardwareentwicklung zu versuchen.
Die Firma Intel verkaufte damals einen Coprozessor für die Gleitkommaarithmetik für den PC für 1200 DM. Von einer amerikanischen Konkurrenzfirma wusste ich, dass die ihr Produkt für 8 Dollar herstellten. Es war also eine gewaltige Gewinnspanne vorhanden.
Wir hatten die Idee, einen wesentlich leistungsfähigeren Arithmetik-Coprozessor für den PC zu entwickeln, welcher Skalarprodukte immer exakt akkumulieren würde. Geeignete Partner waren rasch gefunden. Prof. Höfflinger vom Institut für Mikroelektronik an der Universität Stuttgart und Prof. T. Teufel von der Universität Hamburg/Harburg, der hier bei Prof. Schweizer und mir einmal promoviert hatte. Die VW-Stiftung hatte ein Projekt: Zusammenarbeit im Ingenieur-Bereich ausgeschrieben und wir stellten hier einen Antrag, einen Coprozessor für den IBM-PC mit einem 286-Prozessor zu entwickeln. Die Antragsphase zog sich über zwei Jahre hin. Die beiden Jahre habe ich dazu genutzt, den einen oder anderen Mitarbeiter in einschlägige Vorlesungen zu schicken und sich am Institut für Mikroelektronik in Stuttgart mit den vorhandenen Entwurfs- und Fertigungstechniken vertraut zu machen. Als der Antrag bewilligt wurde, war aus dem 286 im PC bereits der 386 geworden. Die Gleitkommaarithmetik wurde aber immer noch über einen Coprozessor zur Verfügung gestellt. Wir hatten wieder einmal ca. 1 Million DM für ein Forschungsprojekt erhalten.
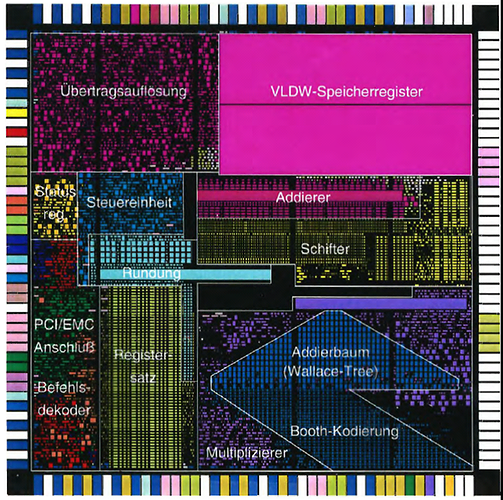
Herr Baumhof hat in Karlsruhe schließlich den Prozessor entworfen. Die Hamburger Gruppe hat die Kopplungs-Elektronik für den PCI- und den EMC-Bus auf den Prozessor integriert und eine entsprechende Platine für den PCI-Bus entworfen und in größeren Stückzahlen gefertigt. In Stuttgart haben dann alle Partner zusammen den endgültigen Chip zusammengestellt und gefertigt, Bild 27, Bild 28.
Zur großen Freude aller Beteiligten waren auf dem ersten Wafer gleich eine größere Anzahl funktionsfähiger Prozessoren enthalten. Unser Prozessor berechnete Skalarprodukte von Vektoren mit Gleitkommakoeffizienten immer exakt und um eine Größenordnung schneller als der PC mit seiner Gleitkommaeinheit ein u.U. falsches Ergebnis.
Herr Höfflinger beauftragte gleich eine Werbeagentur mit dem Entwurf einer entsprechenden Broschüre, Bild 29: Great Architecture, A Vector Arithmetic Coprocessor for the PC.

Das Bild zeigt das Titelblatt einer mehrseitigen Broschüre. Damit ausgestattet reisten Prof. Höfflinger, Herr Baumhof und ich zu einer Computermesse nach Las Vegas und stellten unseren Chip und die Platine dort aus. Ich hatte je ein Exemplar in der Jackentasche. Damit besuchte ich die Stände aller namhaften Hersteller und pries unser Produkt dort an. Überall stieß ich auf großes Interesse. Man bemerkte aber doch eine gewisse Reserviertheit. Wieder nach Deutschland zurückgekehrt, nahm Herr Höfflinger gleich Kontakt mit Banken in Stuttgart auf mit dem Ziel, eine Vermarktung unseres Produktes zu finanzieren. Die Vertreter der Banken aber wollten auch erst wieder die Marktsituation prüfen, und so ging weitere Zeit ins Land.
Ich war froh, dass die Banken nicht gleich bezahlt haben; denn vier Monate später kam Intel mit dem 486 für den PC heraus. Da hatten sie nun die Gleitkommaarithmetik gleich in die CPU mit hinein integriert. Der neue Prozessor lief auch gleich mit 66, dann mit 100 und schließlich mit 400 MHz. Der PCI-Bus, über den wir unsere Einheit anschließen mussten, war für lange Zeit noch bei 33 MHz stehen geblieben. Wir hatten dadurch auch unseren Geschwindigkeitsvorteil eingebüßt.
Wieder hatten wir ein prozessornahes, fortschrittliches und zukunftsweisendes Produkt gebaut und waren, während wir daran arbeiteten, auf der Prozessorseite überholt worden.
Alle vier Episoden, die ich hier geschildert habe, wären mit Sicherheit ganz anders verlaufen, wenn unsere Entwicklung gleichzeitig mit der Entwicklung des zugehörigen Prozessors hätte stattfinden können und unsere Ergebnisse gleichzeitig mit dem Prozessor auf den Markt gebracht worden wären. Die Zusammenarbeit von Intel und Microsoft ist ein klassisches Beispiel dafür. Ein neuer Prozessor und prozessornahe Software müssen gleichzeitig auf den Markt kommen. Nur so hat prozessornahe Software eine Chance.
So etwas ist aber nur möglich, wenn man engen Kontakt zur Prozessorentwicklung haben kann und eng mit dem Prozessorhersteller zusammenarbeitet. Aus all diesen Erfahrungen ergibt sich eine eindeutige Forderung, Bild 30. Die Kulturlandschaft Europa braucht eine eigenständige Rechnerentwicklung.

Die heutige Situation ist für die Kulturlandschaft Europa unwürdig.
Im Jahr der Informatik hat Frau Merkel es so formuliert: Wir haben den Rechner erfunden und andere machen Geschäfte damit. Bei dieser Erkenntnis sollte man nicht stehen bleiben. Man sollte vielmehr aktiv dagegen angehen. Vielleicht liegt hier eine schöne Aufgabe für das inzwischen gegründete KIT in Karlsruhe. Bereits im Jahre 1973 habe ich in einem längeren Brief an das damalige Kernforschungszentrum vorgeschlagen, sich mit Computerhardware zu beschäftigen.
Prof. Krüger wird mir dies bestätigen. Die Antwort lautete: „Wir haben gerade beschlossen, wir machen Software.“ Ich habe damals auch an das Bundesforschungsministerium geschrieben und vorgeschlagen, ein Forschungsprogramm für Mikroelektronik aufzulegen. Die Antwort lautete damals: „Zur Förderung der Mikroelektronik ist es noch zu früh“. Heute bekommt man häufig zur Antwort: „Der Zug ist abgefahren, da hat man keine Chance mehr.“ Dem kann ich nicht zustimmen. Ich meine, es gibt immer wieder Gelegenheit einzusteigen und Besseres zu entwickeln.
Seit 2013 wird die Liste der schnellsten Rechner der Welt von einem Rechner aus China angeführt. Der schnellste Rechner der Jahre 2013, 2014 und 2015 verwendet Prozessoren von Intel. Seine Rechenleistung wird mit 33,86 Petaflops angegeben. Der Spitzenrechner der Jahre 2016 und 2017 verwendet hingegen Prozessoren, welche in China entwickelt und gefertigt werden. Seine Rechenleistung wird mit 93 Petaflops angegeben. Unter Umständen spricht ein Nachfolgerechner später nur noch chinesisch und ist für uns nur noch schwer zugänglich. Der chinesische Markt ist jedenfalls groß genug, um eine derartige Entwicklung zu tragen.
Zum Vergleich: In Europa steht der schnellste Rechner derzeit am Swiss National Super- computing Center. Seine Rechenleistung beträgt 19,6 Petaflops. In 2017 wird er auf Rang 3 gelistet. Er verwendet Prozessoren der Firma Cray Inc. Der in Deutschland z. Zt. schnellste Rechner Hasel Hen steht am HLRS Höchstleistungs-Rechenzentrum in Stuttgart. Seine Leistung wird mit 5,6 Petaflops angegeben. Er verwendet ebenfalls Prozessoren der Firma Cray Inc.
Auf dem Gebiet der Computer Hardware ist in den letzten 50 Jahren ein umfangreiches Wissen entstanden und entwickelt worden, welches weit über eine klassische Ausbildung in Elektrotechnik hinausgeht. Ich habe einmal miterlebt, wie ein Absolvent der Universität von Kyoto in zwei Jahren eine komplette neuartige Arithmetikeinheit für eine Workstation entwickelt hat, oder wie ein Absolvent von Stanford nach zwei Jahren auf einer internationalen Tagung erläutert hat, wie er den nächsten AMD Prozessor entwickelt hat. Diese Leute sind mit den neuesten Entwurfsmethoden und Fertigungstechniken vertraut, wenn Sie die Hochschule verlassen und können sofort in laufenden Produktzyklen eingesetzt werden.
Dieses Niveau müssen auch wir erreichen. Ich halte unsere Studenten nicht für dümmer oder weniger intelligent als diejenigen von der Universität in Kyoto oder von der Waseda-Universität in Tokio, vom MIT oder von Stanford. Das Ganze ist aber auch eine Ausbildungsaufgabe.
Wir haben keine Öl- und Gasquellen, die man nur anzuzapfen braucht und zu Geld machen kann. Unsere Quelle zu Wohlstand sind gute Leute und eine gute und richtige Ausbildung.
In den letzten beiden Jahren meiner aktiven Tätigkeit habe ich in intensiven Verhandlungen mit Vertretern aus vier Fakultäten einen abgestimmten Studienplan Mikroelektronik für unseren Studiengang der Technomathematik ausgearbeitet, den die Fakultät für Mathematik dann auch verabschiedet hat. Inzwischen habe ich festgestellt, dass er wieder aufgegeben wurde.
Zum Schluss möchte ich noch eine Kopie der Umschlagseiten meines neuesten Buches aufzeigen, das im Jahr 2013 in zweiter Auflage erschienen ist, Bild 31. Es enthält viele neue Ideen und Ergebnisse zu den angesprochenen Themen.