Bremsweg
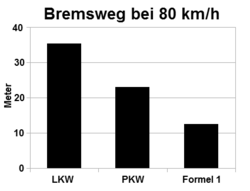
Der Bremsweg wird definiert als Weg, der vom Augenblick des Einleitens der Bremsung bis zum Stillstand des Fahrzeugs bzw. bis zum Erreichen der Endgeschwindigkeit des Bremsvorgangs zurückgelegt wird. Entscheidend für die Länge des Bremsweges sind die anfängliche Geschwindigkeit und die erreichte Bremsverzögerung. Die für den Bremsweg benötigte Zeit ist die Bremszeit (auch als Bremsdauer bezeichnet). Diese (effektive) Bremszeit enthält die Zeit, bis die Bremsreibungskraft volle Stärke erreicht, sowie ggf. Durchschlags-, Umsteuer- und Schlupfzeiten (also Zeiten einer ungebremsten Bewegung).
Der Anhalteweg ist länger als der Bremsweg, denn in ihm ist zusätzlich der Reaktionsweg enthalten, der ungebremst zurückgelegt wird und – neben der Geschwindigkeit – von der Reaktionszeit abhängt.
Für Kraftfahrzeuge (ausgenommen Krafträder) mit einer bauartbedingten Höchstgeschwindigkeit von mehr als 25 km/h hat gemäß § 41 Abs. 4 StVZO die Mindestbremsverzögerung 5 m/s² zu betragen. Bei Schienenfahrzeugen sind Bremswege aufgrund der niedrigeren Bremsverzögerung von etwa 1 m/s² deutlich länger als bei Straßenfahrzeugen.
Berechnung des Bremswegs
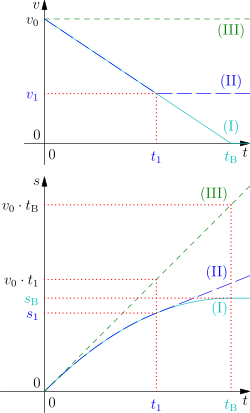
(I): Bremsen von bis zum Stillstand
(II): Bremsen von bis
(III): Fahren mit konstant
Ist die Anfangsgeschwindigkeit (in m/s) zum Zeitpunkt und die als konstant angenommene Bremsverzögerung (in m/s²), dann beträgt der Bremsweg (in m):
- (1)
Für die Momentangeschwindigkeit in Abhängigkeit der Zeit während des Bremsvorgangs () gilt bei einer konstanten Bremsverzögerung:
- (2)
Die Geschwindigkeit nimmt, ausgehend von , linear ab. Dabei ist jener Teil der Geschwindigkeit, der durch das Bremsen „verloren gegangen“ ist. Die hier durch einen positiven Wert ausgedrückte Bremsverzögerung () entspricht einer negativen Beschleunigung.
Für die bis zum Zeitpunkt zurückgelegte Wegstrecke gilt gemäß dem Weg-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung:
- (3)
Bremsen bis zum Stillstand
Kommt der Gegenstand nach der Bremszeit zum Stillstand, dann ist . Dies bedeutet in Gleichung (2):
Löst man diese Gleichung nach der Bremszeit auf, erhält man:
Setzt man die Bremszeit nun in Gleichung (3) ein, so folgt die Beziehung (1) für den Bremsweg :
Bremsen bis zu einer Endgeschwindigkeit
Das Bremsen (mit konstanter Bremsverzögerung ) von der Anfangsgeschwindigkeit (zum Zeitpunkt ) bis zur Endgeschwindigkeit (mit ) führt, analog zu obigen Überlegungen, zur Bremszeit und zum Bremsweg wie folgt:
Bremsen auf der schiefen Ebene
Befindet sich der sich bewegende Gegenstand auf einer geneigten Fahrbahn (schiefen Ebene) mit Neigungswinkel zur Horizontalen (bei Gefälle ), so ist auch der Einfluss der Erdanziehung zu berücksichtigen. Diese bewirkt eine Hangabtriebskraft parallel zur Fahrbahn. Durch die zugehörige Komponente der Erdbeschleunigung parallel zur Fahrbahn ergibt sich die resultierende Verzögerung :
Befindet sich der Gegenstand auf einer ansteigenden Fahrbahn (Neigungswinkel ), so ergibt sich die maximale Bremsverzögerung in Richtung der Fahrbahn zu:
- , wobei der Reibungskoeffizient ist.
Wie oben gilt für den Bremsweg :
Bei Gefälle und glatter Fahrbahn kann die Beschleunigung Null oder negativ werden. Dann wird der Gegenstand nicht gebremst, sondern schneller. Deshalb kann kein Bremsweg angegeben werden.
Kfz-Anhalteweg
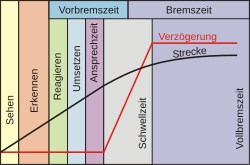
Der Anhalteweg ist die Strecke, die ein Fahrzeug von dem Zeitpunkt, an dem das Hindernis auftritt bzw. gesehen werden kann, bis zum Stillstand zurücklegt. Das Erkennen dauert in der Regel ca. 0,1 s (einen Augenblick). Die Zeit der Reaktion liegt bei etwa 0,8 s. So die Verkehrslage erhöhte Aufmerksamkeit und Reaktionsbereitschaft erfordert, beträgt die Reaktions- und Bremsansprechzeit höchstens 0,6 Sekunden (BGH VRS 6, 13).
Die Ansprechzeit (auch Anlegedauer oder Schlupfzeit) bezeichnet die Zeit von der Betätigung des Bremspedals bis zur ersten Berührung des Bremsbelages mit der Bremsscheibe bzw. -trommel. Während der Ansprechzeit fährt das Fahrzeug mit ungebremster Geschwindigkeit weiter. Die Ansprechzeit kann durch Verringerung des Lüftspiels sowie durch elektronische Sensoren verkürzt werden. Sensor und Steuergerät können eine Notbremsung am schnellen Wechsel von Gas- zu Bremspedal und der hohen Geschwindigkeit der Bremsbetätigung erkennen. Die Bremsung wird durch diese Bremsassistenzsysteme automatisch eingeleitet, Ansprech- und Schwellzeit werden durch raschen Druckaufbau verkürzt.
Die Schwellzeit (d. h. die effektive Bremszeit, siehe Abbildung) ist die Zeit, die die Bremsen benötigen, um die maximale Bremswirkung zu entfalten. Bei einer hydraulischen Bremsanlage liegt die Zeit zwischen 0,1 und 0,2 Sekunden, bei der Druckluftbremsanlage zwischen 0,2 und 0,4 Sekunden. Um die Schwellzeit in Druckluftbremsanlagen zu verringern, werden bremsnah Relaisventile verbaut.
Bei einem Autofahrer wird für die Reaktions- und Vorbremszeit die Dauer von einer Sekunde angenommen. Bei aufmerksamen, geübten Fahrern ist sie kürzer. Drogen, Alkohol und Medikamente verlängern sie deutlich. Die Reaktionszeit bestimmt maßgeblich die Länge des notwendigen Sicherheitsabstands.
Faustformeln
Wird die Geschwindigkeit durch die Einheit km/h dividiert, erhält man den Zahlenwert
- .
Der zurückgelegte Weg wird durch die Einheit m dividiert und man erhält den Zahlenwert
- .
In Deutschland werden bei der Führerscheinprüfung die folgenden Faustformeln verwendet:
- Reaktionsweg
Das heißt, es wird etwa eine Sekunde Reaktionszeit angenommen.
Man unterscheidet zwischen Normalbremsung und Gefahrbremsung. Tatsächliche Werte sind abhängig von Fahrzeugtyp, Wetter, Straßenzustand und Fahrer.
- Bremsweg bei Normalbremsung (Verzögerung ca. 3,9 m/s²)
- Bremsweg bei Gefahrbremsung (Verzögerung ca. 7,7 m/s²)
- Beispiele
- Bei einer Geschwindigkeit von = 50 km/h auf trockener Fahrbahn im Ortsgebiet ergibt sich bei Normalbremsung das ergibt einen Reaktionsweg von und und somit einen Bremsweg von – die Summe aus beiden, der Anhalteweg, beträgt also etwa 40 Meter.
- Bei einer Gefahrenbremsung ergibt sich ein Anhalteweg von .
- Sicherheitsabstand in Meter
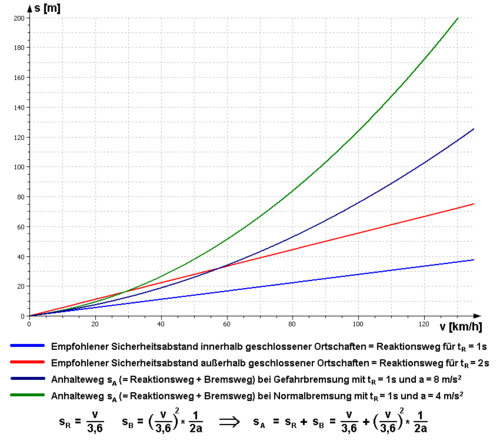
Der Sicherheitsabstand kann – als Ein- bzw. Zwei-Sekunden-Abstand, modifiziert durch die Witterung – überschlagsmäßig mit der Faustformel
berechnet werden, wobei von der Straßensituation abhängt (trockene Fahrbahn: ); im Ortsgebiet ist eine Mindest-Zeit von und im Freiland von einzuhalten. Bei nasser Fahrbahn wird etwa der 1,5-fache bis doppelte Abstand (k = 1,5…2) und bei Schnee sowie Rollsplitt wird der etwa vierfache Abstand (k = 4) benötigt. Bei Glatteis ist der Bremsweg noch deutlich länger. Die Zahl 4 in der Faustformel stellt eine Näherung für die 3,6 aus der Umrechnung von km/h in m/s dar.
- Beispiele
- Innerorts (t = 1 s) gilt bei trockener Fahrbahn (k = 1) mit v = 50 km/h für den Sicherheitsabstand etwa , also .
- Außerorts (t = 2 s) ergibt die Formel für trockene Fahrbahn (k = 1) den bekannten halben Tacho in Metern, also Sicherheitsabstand , also .
Schienenverkehr
Bei Zügen ist die Bremsverzögerung ca. 1 m/s², was sich durch die geringere Reibung zwischen den Metalloberflächen Rad und Schiene ergibt. Bei gleicher Anfangsgeschwindigkeit ist der Bremsweg eines Zuges etwa um den Faktor zehn länger als der eines Autos. Der Bremsweg eines 90 km/h fahrenden Haltezuges hat eine Länge von über 313 Metern. Schnellzüge fahren in den Niederlanden mit Geschwindigkeiten von 110–125 km/h und haben einen Mindestbremsweg von mehr als einem halben Kilometer. Hochgeschwindigkeitszüge fahren mit Geschwindigkeiten von 220–320 km/h, was bedeutet, dass ihr minimaler Bremsweg eine Länge von zwei bis mehr als fünf Kilometer erreicht.
Für Eisenbahnstrecken wird ein bestimmter Bremswegabstand festgelegt, innerhalb dessen jeder Zug anhalten können muss. Abhängig vom Bremsvermögen eines Zuges wird so seine zulässige Höchstgeschwindigkeit bestimmt. In Deutschland geschieht dies anhand einer Bremstafel.
Als Bremskurve wird der Verlauf der Soll-Geschwindigkeit in Abhängigkeit vom zurückgelegten Bremsweg bezeichnet. Das Einhalten dieser Kurve wird durch Zugbeeinflussungssysteme überwacht, die sicherstellen, dass ein Zug rechtzeitig zum Halten kommt oder seine Geschwindigkeit reduziert hat.
Schiffe
Schiffe werden hauptsächlich durch gezielte Erhöhung des hydrodynamischen Widerstandes gebremst. Es sind jedoch auch andere Mittel wie das Auswerfen von Ankern und ein geeignetes Verstellen von Segeln zur Verringerung der Geschwindigkeit möglich.
Das hauptsächlich angewendete Verfahren zum aktiven Bremsen besteht in der Schubumkehr des Antriebes. Dazu werden im Fall von Schiffsschrauben und Schaufelrädern die Drehrichtung umgekehrt, bei Wasserstrahlantrieben der Strahl umgelenkt. Da Schiffe relativ schwer sind und das Medium Wasser mit der relativ niedrigen Viskosität nur einen geringen Strömungswiderstand bietet, bremsen – große – Schiffe im Vergleich zu Autos und Zügen meist langsamer. Schiffe mit einem hohen Verhältnis von Motorleistung pro Masseneinheit wie leichte Kreuzer und Schlepper haben deshalb eine vergleichsweise hohe Bremsverzögerung.
Je kleiner ein Boot ist, desto schneller wird es vom Strömungswiderstand abgebremst: Ein Ruder-Achter läuft ohne Riemenschlag mehrere Dutzend Meter aus. Ein Einer-Kajak oder kleines Schlauchboot läuft ohne Paddelschlag nur wenige Meter. Die Internationale Seeschifffahrts-Organisation schreibt vor, dass Schiffe bei einem Nothaltmanöver aus voller Fahrt innerhalb von 15 (in Ausnahmefällen 20) Schiffslängen zum Stehen kommen müssen. Ein solches Manöver belastet allerdings die Hauptmaschine, ihre Fundamentierung und die Welle so stark, dass dies außer bei der technischen Abnahme nur im Ausnahmefall praktiziert wird. Aus den Regularien ergäbe sich bei maximalen 450 m Schiffslänge eine Strecke von höchstens 9 km (4,9 sm) zum Stillstand dieses Fahrzeugs im Notfall.
Weblinks
License Information of Images on page#
| Image Description | Credit | Artist | License Name | File |
|---|---|---|---|---|
| Bremsvorgangsphasen | Eigenes Werk | Stefan-Xp | Datei:Bremsvorgang.svg | |
| based loosely on this Bremsweg bei 80 km/h in Meter LKW 40 to, PKW, Formel 1 Jeweils voll beladen Aktuelle Testwerte von ADAC.de 9/2015 und von Auto Motor und Sport Graustufenbild. Arial 12 fett. | Eigenes Werk | User:Alex42 | Datei:Bremsweg80kmh.png | |
| Funktionsgraphen (im kartesischen Koordinatensystem ) der zeitlichen Verläufe von Geschwindigkeit v \displaystyle v (oberes Diagramm) und dabei zurückgelegter Wegstrecke s \displaystyle s (unteres Diagramm) zur Veranschaulichung des Bremswegs für die drei folgenden Fälle: Kurven (I) : Bremsen (mit konstanter Bremsverzögerung a > 0 \displaystyle a>0 ) von der Anfangsgeschwindigkeit v 0 = v ( 0 ) \displaystyle v_0=v(0) (zum Zeitpunkt t 0 = 0 \displaystyle t_0=0 ) bis zum Stillstand führt nach verstrichener Bremszeit t B \displaystyle t_\textB zum Bremsweg s B = s ( t B ) \displaystyle s_\textB=s(t_\textB) : v ( t ) = v 0 − a ⋅ t , wenn 0 ≤ t < t B , 0 , wenn t ≥ t B , \displaystyle v(t)=\begincasesv_0-a\cdot t,&\textwenn 0\leq t<t_\textB\text, 0,&\textwenn t\geq t_\textB\text,\endcases mit t B = v 0 a \displaystyle t_\textB=\frac v_0a s ( t ) = v 0 ⋅ t − 1 2 ⋅ a ⋅ t 2 , wenn 0 ≤ t < t B , s B , wenn t ≥ t B , \displaystyle s(t)=\begincasesv_0\cdot t-\frac 12\cdot a\cdot t^2,&\textwenn 0\leq t<t_\textB\text, s_\textB,&\textwenn t\geq t_\textB\text,\endcases mit s B = v 0 2 2 ⋅ a \displaystyle s_\textB=\frac v_0^22\cdot a Kurven (II) : Bremsen (mit konstanter Bremsverzögerung a > 0 \displaystyle a>0 ) von der Anfangsgeschwindigkeit v 0 = v ( 0 ) \displaystyle v_0=v(0) (zum Zeitpunkt t 0 = 0 \displaystyle t_0=0 ) bis zur Endgeschwindigkeit v 1 = v ( t 1 ) \displaystyle v_1=v(t_1) (mit 0 ≤ v 1 < v 0 \displaystyle 0\leq v_1<v_0 ) führt nach verstrichener Bremszeit t 1 \displaystyle t_1 zum Bremsweg s 1 = s ( t 1 ) \displaystyle s_1=s(t_1) : v ( t ) = v 0 − a ⋅ t , wenn 0 ≤ t < t 1 , v 1 , wenn t ≥ t 1 , \displaystyle v(t)=\begincasesv_0-a\cdot t,&\textwenn 0\leq t<t_1\text, v_1,&\textwenn t\geq t_1\text,\endcases mit t 1 = v 0 − v 1 a \displaystyle t_1=\frac v_0-v_1a s ( t ) = v 0 ⋅ t − 1 2 ⋅ a ⋅ t 2 , wenn 0 ≤ t < t 1 , s 1 + v 1 ⋅ ( t − t 1 ) , wenn t ≥ t 1 , \displaystyle s(t)=\begincasesv_0\cdot t-\frac 12\cdot a\cdot t^2,&\textwenn 0\leq t<t_1\text, s_1+v_1\cdot (t-t_1),&\textwenn t\geq t_1\text,\endcases mit s 1 = v 0 ⋅ t 1 − 1 2 ⋅ a ⋅ t 1 2 = v 0 2 − v 1 2 2 ⋅ a \displaystyle s_1=v_0\cdot t_1-\frac 12\cdot a\cdot t_1^2=\frac v_0^2-v_1^22\cdot a Kurven (III) : Zum Vergleich: Fahren mit konstanter Geschwindigkeit v 0 \displaystyle v_0 ohne jegliche Verzögerung oder Beschleunigung. Hier kann kein Bremsweg angegeben werden. v ( t ) = v 0 \displaystyle v(t)=v_0 für t ≥ 0 \displaystyle t\geq 0 s ( t ) = v 0 ⋅ t \displaystyle s(t)=v_0\cdot t für t ≥ 0 \displaystyle t\geq 0 | Eigenes Werk | SweetWood | Datei:Graphs of speed and displacement during braking with constant deceleration.svg | |
| Sicherheitsabstände und Anhaltewege in Abhängigkeit von der Fahrzeuggeschwindigkeit | Eigenes Werk | Qniemiec | Datei:Safety and stopping distances de.png | |
| Datei:Wiktfavicon en.svg |


























































