Kreuzgelenk

Die Achsen des Zwischenstücks schneiden sich.
Ein Kreuzgelenk (auch Kardangelenk oder Universalgelenk) ist eine winkelbewegliche Kupplung zwischen zwei Wellen zu einer sogenannten Kardanwelle. Der Beugungswinkel zwischen den angeschlossenen Wellen darf sich während der Drehmoment-Übertragung verändern.
Im Gegensatz zu dem Gleichlaufgelenk und der Metallbalgkupplung übertragen Kreuzgelenke die Winkelgeschwindigkeit nicht gleichmäßig.
Kardangelenke, die nicht der Übertragung von Drehungen oder Drehmomenten dienen, werden im Artikel Kardanische Aufhängung behandelt.
Geschichte
Eine der ersten genauer überlieferten Anwendungen fand sich in der Uhr des Straßburger Münsters von 1354, über die Caspar Schott 1664 berichtete. Mit dem Namen Gerolamo Cardano ist seit etwa 1550 die später (vorwiegend im europäischen Raum) als „kardanische Aufhängung“ bezeichnete bewegliche Aufhängung bekannt geworden, wobei Cardano selbst schrieb, dass er von einer ähnlichen Vorrichtung inspiriert worden sei. Bereits seit 1245 ist von Villard de Honnecourt eine Aufhängung für einen Ofen bekannt und um 1500 hängte Leonardo da Vinci auf gleiche Weise einen Kompass auf.
Der englische Universalgelehrte Robert Hooke erfand 1663 die Kreuzgelenke in einer Vorform. Er hatte ihre ungleichförmige Übertragung erkannt und die Kombination zu einem Doppelkreuzgelenk entwickelt, welche diese Ungleichförmigkeit durch Kombination zweier Einzelgelenke zum Doppelkreuzgelenk zu einem großen Teil kompensierte. Im angelsächsischen Sprachraum sind Kreuzgelenke bis heute als „Hooke’s Joint“ („Hookesches Gelenk“) bekannt.
Kreuzgelenke in der heutigen Form mit einem Zapfenkreuz gehen auf Amicus (16. Jahrhundert) zurück. Den mathematischen Beweis der ungleichförmigen Drehung legte 1824 Jean-Victor Poncelet vor.[1]
Funktion und Anwendungen
Ein zentrales Teil (Kreuzstück) enthält zwei rechtwinklig gekreuzte Achsstummel-Paare, über die es mit je einer der beiden Wellen gelenkig verbunden ist: Die Wellen haben je ein gabelförmiges Ende, deren Querbohrungen je ein Achsstummel-Paar umfassen. Eine seltenere Variante, bei der eine der beiden Wellen im Inneren des zentralen Teils angelenkt ist, erinnert an die kardanische Aufhängung (bei der kardanischen Aufhängung eines Kreisels (Kreiselkompass) befindet sich ganz im Inneren noch eine dritte Welle, um die der Kreisel rotiert).
Eine bauliche Einheit aus Kardangelenk/en und Welle/n wird als Kardanwelle bezeichnet. Diese dient traditionell zur Drehmoment-Übertragung in Kraftwagen zwischen der Einheit Motor/Getriebe und Hinterachse. Die Welle überbrückt die beträchtliche Distanz. Bei federnder Bewegung der Hinterachse erfährt das Kardangelenk (oder die Kardangelenke) eine kleine Beugung.
Bei einer am Traktor angehängten Arbeitsmaschine, die selbst fährt, ist die Auslenkung zwischen Traktor und Maschine relativ hoch. Der Zapfwelle am Traktor folgt ein Doppelkreuzgelenk mit Zwischenwelle (Doppelgelenkwelle).
-
Kreuzgelenk zwischen Lenksäule und Lenkgetriebe
-
Kardangelenke (links unten) sind ein typisches Zubehörteil in einem Steckschlüssel-Satz. Die Achsen des komprimierten Zwischenstücks kreuzen, schneiden sich aber doch nicht.
Kardanfehler
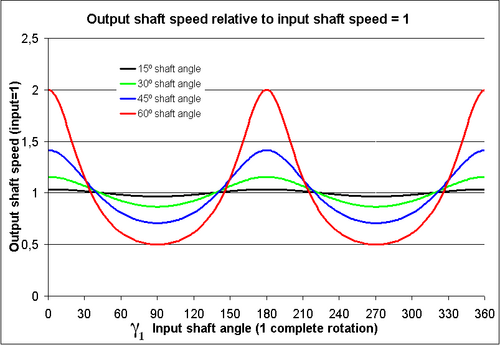
Links ist die Winkelgeschwindigkeit (Ro ta tions ge schwin dig keit) der Abgangswelle des Gelenks angetragen, im Verhältnis zur Stellung der Eingangswelle. Die rote Kurve zeigt, dass die Geschwindigkeit der Abgangswelle während einer Umdrehung zweimal auf das Doppelte der Ge schwin dig keit der Eingangswelle beschleunigt und zweimal wieder auf die Hälfte abgebremst wird, wenn das Gelenk stark abgewinkelt ist (hier um 60°).
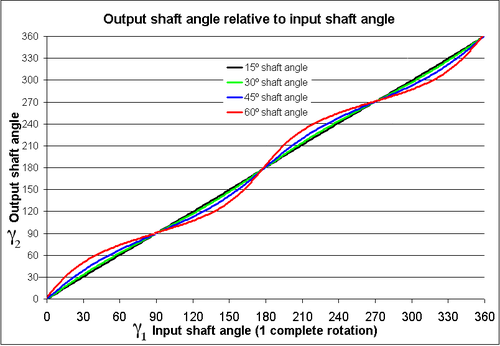
Ein gebeugtes Kreuzgelenk bewirkt eine ungleichmäßige Drehübertragung. Das bedeutet, dass bei konstanter Drehgeschwindigkeit der Antriebswelle die Abtriebswelle keine konstante Drehgeschwindigkeit hat. Diese Ungleichmäßigkeit, die auch Kardanfehler genannt wird, nimmt mit dem Beugewinkel stark zu.[2] Das momentane Verhältnis der Drehgeschwindigkeiten und , auch als (momentane) Übersetzung bezeichnet, ist bei momentanem Drehwinkel [3] der Antriebswelle:
- . [4]
Die Abtriebswelle dreht sich während einer Umdrehung zweimal etwas schneller und zweimal etwas langsamer als die Antriebswelle, so dass die Durchschnittsdrehzahl der Abtriebswelle wiederum der Drehzahl der Antriebswelle entspricht.
Gelegentlich wird auch die Differenz der Drehwinkel als Kardanfehler bezeichnet.
Der Drehwinkel hängt nach folgender Gleichung vom Drehwinkel und dem Beugewinkel ab:
- . [4]
Die Ungleichförmigkeit bewirkt bei Kraftübertragung nicht nur eine Belastung der Lager, nachteilig sind auch eine ungleichförmige Drehmomentübertragung und auftretende Schwingungen. Die Ungleichförmigkeit wirkt sich umso stärker negativ aus, je größer Drehzahl, Beugewinkel und Belastung der Gelenkwelle sind.[5] Deshalb sind Kreuzgelenke beispielsweise zur Kraftübertragung bei Kraftfahrzeugen mit Frontantrieb und gelenkter Vorderachse grundsätzlich ungeeignet.
Herleitung der Formeln
Im Kreuzgelenk werden zwei Achsen miteinander verbunden, die sich jeweils drehen. Dabei ist der Rotationswinkel der ersten Achse , der der zweiten und der Winkel, um den die beiden Achsen gegeneinander abgeknickt sind. beschreibt dabei, dass sie in einer Geraden liegen.
-
Achsenstücke und zugehörige Rotationsebenen
-
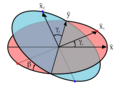
Rotationsebenen mit den verwendeten Vektoren
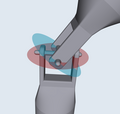
Im Diagramm rechts sind diese Winkel, das ortsfeste Koordinatensystem , und die beiden Punkte und eingezeichnet. Dabei sind und die normierten Vektoren von der Zwischenstückmitte zu den Verbindungspunkten zwischen diesem und dem Achsstück 1, beziehungsweise 2. Durch Drehen der Achse 1 bewegt sich in der rot eingezeichneten Ebene um und in der blauen Ebene um .
Wie oben im Diagramm zu erkennen ist, sind die Koordinaten der Vektors und im -Koordinatensystem gegeben durch
und
- .
Durch die Bauart des Zwischenstücks bedingt, stehen und senkrecht aufeinander, also ist .
Daher stehen die Winkel , , in folgendem Zusammenhang:
Für gilt damit
Ableiten der Formel liefert mit und und
Vermeidung des Kardanfehlers durch Doppelgelenke
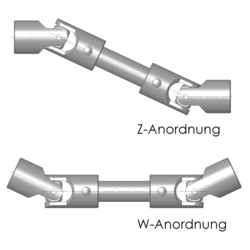

Zwei hintereinander angeordnete Kreuzgelenke ergeben eine Doppelgelenkwelle.[6] Bei gleichen Beugewinkeln an beiden Gelenken können sich die Kardanfehler am ersten und zweiten Gelenk gegeneinander ausgleichen. Dazu müssen die Gelenkgabeln des Zwischenstücks den richtigen Winkel zueinander haben. Wenn An- und Abtriebswelle parallel zueinander stehen („Z-Anordnung“), müssen auch die Achsen der beiden Gabeln des Zwischenstücks parallel zueinander sein (Die Antriebsgabel des ersten Gelenks steht um 90° versetzt zur Antriebsgabel des zweiten Kreuzgelenks). Wenn An- und Abtriebswelle nicht in einer Ebene liegen, dann müssen die Gabelachsen des Zwischenstücks um den Winkel gegeneinander verdreht sein, der zwischen den durch Zwischenstück und An- und Abtriebswelle definierten Ebenen ansteht. Beträgt dieser Winkel 180°, dann schneiden sich die Achsen von An- und Abtriebswelle („W-Anordnung“; immer noch gilt: gleiche Beugewinkel) und die Achsen der beiden Gabeln des Zwischenstücks stehen wieder parallel.
Die Z-Anordnung mit parallelen Drehachsen an An- und Abtrieb wird in Fahrzeugen (Lkw) zur Kraftübertragung zwischen Getriebe und Antriebsachse angewendet. Andere Konstellationen finden sich in Fahrzeugen an der Lenksäule.
Die W-Anordnung, bei der beide Gelenke in die gleiche Richtung knicken, ist die Grundlage von Doppelkreuzgelenken und Tracta- wie Scharniergelenken.
Auch bei einer Doppelgelenkwelle mit zwei Kreuzgelenken lässt sich der Kardanfehler nicht ganz vermeiden: Er wirkt weiterhin auf die Verbindungswelle, die regelmäßig beschleunigt und abgebremst wird. Dies belastet die Lager, und Oszillation der Zwischenwelle kann unter ungünstigen Umständen trotzdem zu Vibrationen führen. Letztere können durch die Verwendung von Gummigelenken oder zwischengeschalteten Gummielementen weiter reduziert werden. Je kleiner die Masse der Verbindungswelle ist, desto geringer sind die Auswirkungen der Ungleichförmigkeit. Beim Doppelkreuzgelenk sind zwei Kreuzgelenke direkt hintereinander angeordnet, hier ist die Ungleichförmigkeit auf einen inneren Mitnehmer beschränkt, sodass sie den Gleichlaufgelenken zugeordnet werden können. Möglich sind ferner Kreuzgelenke mit Korrekturgliedern, die Geschwindigkeitsänderungen ausgleichen, diese sind aufgrund ihrer Komplexität jedoch wenig verbreitet.[5]
Siehe auch
- Kardanwelle
- Kardanantrieb bei Motorrädern
- Eine Hardyscheibe lässt ebenso wie das Kreuzgelenk einen Winkelversatz zwischen An- und Abtriebswelle zu, besteht jedoch lediglich aus einer sich verformenden elastischen Scheibe und benötigt keine Drehlager.
Literatur
- Hans-Christoph von Seherr-Thoss, Friedrich Schmelz, Erich Aucktor: Gelenke und Gelenkwellen. Berechnung, Gestaltung, Anwendungen, Springer, 2. erweiterte Auflage 2002. ISBN 3-540-41759-1.
- Siegfried Hildebrand: Feinmechanische Bauelemente, Hanser, 1968.
Weblinks
- Eugen Klein GmbH: Die Kinematik des Kreuzgelenkes
- O. Fischer: Kinematik des Kreuzgelenkes
Anmerkungen und Einzelnachweise
- ↑ Historische Daten nach „Gelenke und Gelenkwellen“, siehe Literatur
- ↑ Kardan Theorie auf der Seite Powerboxer.de; abgerufen im September 2016
- ↑ Die nachfolgenden Gleichungen und Grafiken gelten für die sogenannte „nullphasige“ Anfangslage: γ1 = 0°, wenn sich die antriebsseitige Achse des Kardankreuzes in der Ebene der beiden Wellen befindet.
- 1 2 3 4 Siegfried Hildebrand: Feinmechanische Bauelemente, Carl Hanser Verlag, 1968, Seite 725
- 1 2 PKW-Radantriebswellen. In: Kraftfahrzeugtechnik 4/1980, S. 114–116; mit Abbildungskorrektur in 8/1980, S. 245.
- ↑ Kardan Theorie auf der Seite Powerboxer.de; abgerufen im September 2016
License Information of Images on page#
| Image Description | Credit | Artist | License Name | File |
|---|---|---|---|---|
| Draufsicht zweier Gelenkwellen mit zwei Wellengelenken nach DIN 808 (Typ E, Einfachgelenk) . Die Befestigung der Wellengelenke erfolgt hier durch Kegelstifte . | created by Silberwolf ( talk ) | Silberwolf ( talk ) | Datei:Cardan-joint intermediate-shaft topview de.png | |
| The Wikimedia Commons logo, SVG version. | Original created by Reidab ( PNG version ) SVG version was created by Grunt and cleaned up by 3247 . Re-creation with SVG geometry features by Pumbaa , using a proper partial circle and SVG geometry features. (Former versions used to be slightly warped.) | Reidab , Grunt , 3247 , Pumbaa | Datei:Commons-logo.svg | |
| Hexapod in general animated depiction | Übertragen aus de.wikipedia nach Commons. Originally uploaded at de:Bild:Hexapod allgemein Anim.gif Eigenes Werk . Created with Autodesk Inventor | UtzOnBike in der Wikipedia auf Deutsch | Datei:Hexapod general Anim.gif | |
| Datei:Merge-arrows.svg | ||||
| Socket wrench, universal joint and sockets | Eigenes Werk | Kae | Datei:Socket wrench and sockets.JPG | |
| Diagram of variables for the universal joint. The axis of axle 1 is perpendicular to the red plane and the axis of axle 2 is perpendicular to the blue plane, which are at an angle β with respect to each other. The angular displacement of each axle is given by γ 1 \displaystyle \gamma _1 and γ 2 \displaystyle \gamma _2 respectively, which are the angles of the unit vectors x ^ 1 \displaystyle \hat x_1 and x ^ 2 \displaystyle \hat x_2 with respect to their initial positions along the x and y axes respectively. The x ^ 1 \displaystyle \hat x_1 and x ^ 2 \displaystyle \hat x_2 vectors are fixed in the gymbal which connects the two joints and so are constrained to remain perpendicular to each other at all times. | Eigenes Werk | user:PAR | Datei:UJoint.png | |
| This is a replacement file for Image:Universal joint - output speed relative to input speed.png. It is the same image, but shifted 90 degrees in order to conform to the more detailed analysis presented. | created by user:PAR | user:PAR | Datei:UJoint1.png | |
| This is a replacement file for Image:Universal joint - output angle relative to input angle.png. It is the same image, but shifted 90 degrees in order to conform to the more detailed analysis presented. | created by user:PAR | user:PAR | Datei:UJoint2.png | |
| A sample universal joint colour-coded to the diagrams about the equation of motion. The red and blue planes are visible. | Eigenes Werk | Not Thomas Edison | Datei:UJoint 3D.png | |
| Datei:Universal joint.png |
















![{\displaystyle {\hat {\mathbf {x} }}_{1}=\left[\cos \gamma _{1}\,,\,\sin \gamma _{1}\,,\,0\right]}](/aw/img/svg/29b84fdcd5b6bc07d771b025df6ccac73e27c185)
![{\displaystyle {\hat {\mathbf {x} }}_{2}=\left[-\cos \beta \sin \gamma _{2}\,,\,\cos \gamma _{2}\,,\,\sin \beta \sin \gamma _{2}\right]}](/aw/img/svg/a7c672bb06806fbbef22b24b171fca3c4f5ad4c1)









