Der Massenmittelpunkt (auch Schwerpunkt oder manchmal zur Unterscheidung vom Formschwerpunkt auch Gewichtsschwerpunkt genannt) eines Körpers ist das mit der Masse gewichtete Mittel der Positionen seiner Massepunkte. Für kontinuierliche Massenverteilungen wird das Ortsmittel der Dichte als Massenmittelpunkt definiert. Bei einem homogenen Körper (d. h. bei überall gleicher Dichte) stimmt der Massenmittelpunkt mit dem geometrischen Schwerpunkt überein. Das Stehaufmännchen bildet ein Beispiel für einen inhomogenen Körper.

Das Konzept des Massenmittelpunktes dient in der Physik der Reduktion eines komplexen ausgedehnten starren Körpers auf einen einzigen Massepunkt zur einfacheren Berechnung seiner Bahnkurve bei Einwirkung einer Kraft. Auch vereinfachen sich viele Rechnungen im Schwerpunktsystem, in dem der Massenmittelpunkt als Koordinatenursprung verwendet wird (siehe auch Mehrkörpersystem). Im Massenmittelpunkt angreifende externe Kräfte können den Rotationszustand des Objekts nicht verändern, da sie wegen des im Schwerpunkt fehlenden Hebelarms kein Drehmoment ausüben. Achsen durch den Schwerpunkt werden auch als Schwerachsen bezeichnet.^[1]

In der Himmelsmechanik bezeichnet man den Massenmittelpunkt eines Systems von mehreren Himmelskörpern als Baryzentrum.

Der Massenmittelpunkt eines Körpers muss nicht im Inneren des Körpers liegen. Beispiele dafür sind der Torus, ein Bumerang, eine Tasse oder der Körperschwerpunkt eines Hochspringers. Ist der Körper aber konvex, so liegt der Schwerpunkt niemals außerhalb.

Massenschwerpunkt zweier Punktmassen auf einem Stab

Gegeben sei ein Stab der Länge ${\displaystyle a}$. Auf diesem Stab befinden sich die zwei Punktmassen ${\displaystyle m_{1}}$ und ${\displaystyle m_{2}}$ an den Orten ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$.

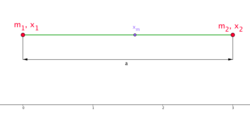
Der Massenschwerpunkt (Massenmittelpunkt) ${\displaystyle x_{s}}$ lässt sich dann wie folgt berechnen:

${\displaystyle x_{s}={\frac {m_{2}}{m_{1}+m_{2}}}\cdot a}$

Das Massenverhältnis ist sozusagen ein prozentualer Faktor zu ${\displaystyle a}$. Wird die Masse ${\displaystyle m_{2}}$ unendlich groß, so verschiebt sich der Massenschwerpunkt an den Ort ${\displaystyle x_{2}}$. Wird jedoch die Masse ${\displaystyle m_{1}}$ im Verhältnis zu ${\displaystyle m_{2}}$ unendlich groß, so verschiebt sich der Massenschwerpunkt an den Ort ${\displaystyle x_{1}}$.

Etwas Allgemeiner:

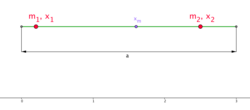
Aus Bild 1 ist zu erkennen, dass ${\displaystyle a=x_{2}-x_{1}}$ gilt. In Bild 2 sind nun die Punktmassen nicht mehr am Anfangs- und Endpunkt des Stabes. Da in den Bildern die Skala von links nach rechts verläuft muss man also den Abstand zwischen dem Anfangspunkt des Stabes und dem Massenpunkt ${\displaystyle x_{1}}$ dazu addieren. Somit kommt man zu folgender Formel:

${\displaystyle x_{s}={\frac {m_{2}}{m_{1}+m_{2}}}\cdot (x_{2}-x_{1})+x_{1}={\frac {x_{1}\cdot m_{1}+x_{2}\cdot m_{2}}{m_{1}+m_{2}}}}$

Massenschwerpunkt mehrerer Punktmassen auf einem Stab

Um dies vom vorherigen Abschnitt fortzusetzen platzieren wir nun 3 Punktmassen auf einem Stab.

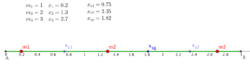
Um den Massenschwerpunkt zu bestimmen, zerlegen wir dieses Konstrukt in 2 Teilstäbe. Dazu durchtrennen wir den Stab am Ort ${\displaystyle x_{2}}$ und teilen die Masse ${\displaystyle m_{2}}$ zur Hälfte auf den einen Teilstab und die andere Hälfte auf den anderen Teilstab auf. Zunächst berechnen wir wie folgt die Massenschwerpunkte der Teilstäbe wie aus dem vorherigen Abschnitt bekannt:

${\displaystyle x_{s1}={\frac {0{,}5\cdot m_{2}}{m_{1}+0{,}5\cdot m_{2}}}\cdot (x_{2}-x_{1})+x_{1}}$

${\displaystyle x_{s2}={\frac {m_{3}}{0{,}5\cdot m_{2}+m_{3}}}\cdot (x_{3}-x_{2})+x_{2}}$

Nun kann man mit der Gesamtmasse der Teilstäbe und dem Massenschwerpunkt die Teilstäbe als neue Punktmasse zusammenfassen:

${\displaystyle m_{xs1}=m_{1}+0{,}5\cdot m_{2}}$

${\displaystyle m_{xs2}=0{,}5\cdot m_{2}+m_{3}}$

Nun berechnet man mit diesen neuen Werten einen weiteren Massenschwerpunkt, welche schlussendlich der Massenschwerpunkt der drei Punktmassen ist:

${\displaystyle x_{s}={\frac {m_{xs2}}{m_{xs1}+m_{xs2}}}\cdot (x_{s2}-x_{s1})+x_{s1}}$

Eingesetzt sieht das dann wie folgt aus:

${\displaystyle {x_{s}={\frac {0{,}5\cdot m_{2}+m_{3}}{m_{1}+m_{2}+m_{3}}}\cdot \left({\frac {m_{3}\cdot (x_{3}-x_{2})}{0{,}5\cdot m_{2}+m_{3}}}+x_{2}-{\frac {0{,}5\cdot m_{2}\cdot (x_{2}-x_{1})}{m_{1}+0{,}5\cdot m_{2}}}-x_{1}\right)+{\frac {0{,}5\cdot m_{2}\cdot (x_{2}-x_{1})}{m_{1}+0{,}5\cdot m_{2}}}+x_{1}}}$

Formt man diese Gleichung etwas um, kommt man zu folgendem Ergebnis:

${\displaystyle x_{s}={\frac {x_{1}\cdot m_{1}+x_{2}\cdot m_{2}+x_{3}\cdot m_{3}}{m_{1}+m_{2}+m_{3}}}}$

Vergleicht man dieses Ergebnis mit dem aus vorherigen Abschnitt, so ist eine Regelmäßigkeit zu erkennen. Verteilt man nun n-viele Punktmassen auf einem Stab so lässt sich der Massenschwerpunkt wie folgt bestimmen:

${\displaystyle x_{s}={\frac {1}{M}}\cdot \sum _{i=1}^{n}{x_{i}\cdot m_{i}}}$

Dabei ist ${\displaystyle M}$ die Gesamtmasse, sprich die Summe aller Punktmassen:

${\displaystyle M=\sum _{i=1}^{n}{m_{i}}}$

Massenschwerpunkt bei kontinuierlicher Massenverteilung entlang eines Stabes

Hier greifen wir auf die Formel aus vorherigem Abschnitt zurück und bilden den Grenzwert. Damit erhält man eine integrale Darstellung.

Massenschwerpunkt:

${\displaystyle x_{s}={\frac {1}{M}}\cdot \int _{x_{1}}^{x_{2}}{x\cdot \mathrm {d} m}={\frac {1}{M}}\cdot \int _{x_{1}}^{x_{2}}{x\cdot \lambda (x)\mathrm {d} x}}$

Dichtefunktion:

${\displaystyle {\frac {\mathrm {d} m}{\mathrm {d} x}}=\lambda (x)}$

Gesamtmasse:

${\displaystyle M=\int _{x_{1}}^{x_{2}}{\lambda (x)\mathrm {d} x}}$

Mathematische Definition

Der Massenmittelpunkt ${\displaystyle {\vec {r}}_{s}}$ ist das mit der Masse gewichtete Mittel der Ortsvektoren ${\displaystyle {\vec {r}}}$ aller Massepunkte ${\displaystyle \mathrm {d} m}$ eines Körpers:

${\displaystyle {\vec {r}}_{s}={\frac {1}{M}}\int _{K}{{\vec {r}}\,\mathrm {d} m}={\frac {1}{M}}\int _{K}{{\vec {r}}\,\rho ({\vec {r}})\,\mathrm {d} V}}$

Dabei ist ${\displaystyle \rho ({\vec {r}})}$ die Dichte am Ort ${\displaystyle {\vec {r}}}$ und ${\displaystyle dV}$ ein Volumenelement. Der Nenner ${\displaystyle M}$ dieser Terme ist die Gesamtmasse.

Bei einem homogenen Körper kann die Dichte ${\displaystyle \rho }$ als Faktor vor das Integral gezogen werden, der Massenmittelpunkt fällt dann mit dem Volumenmittelpunkt (dem geometrischen Schwerpunkt) zusammen. In vielen Fällen kann die Berechnung dann vereinfacht werden; beispielsweise, wenn der Volumenmittelpunkt auf einer Symmetrieachse des Körpers liegt, zum Beispiel bei einer Kugel im Mittelpunkt.

Bei diskreten Systemen kann das Volumenintegral durch eine Summe über die Ortsvektoren ${\displaystyle {\vec {r}}_{i}}$ aller Massepunkte ersetzt werden:

${\displaystyle {\vec {r}}_{s}={\frac {1}{M}}\sum _{i}m_{i}\,{\vec {r}}_{i}}$

wobei ${\displaystyle M}$ die Summe aller Einzelmassen ${\displaystyle m_{i}}$ ist:

${\displaystyle M=\sum _{i}m_{i}}$

Der Begriff Massenmittelpunkt im Vergleich zum Gravizentrum

Die Gravitation wirkt auf alle Massenpunkte eines Körpers. Nur in einem homogenen Gravitationsfeld ist die Gesamtwirkung so, als würde die Gravitationskraft im Massenmittelpunkt angreifen. Da das Gravitationsfeld oft als homogen angenommen werden kann, z. B. in der Nähe der Erdoberfläche, werden die Begriffe Gravizentrum und Massenmittelpunkt oft beide undifferenziert als Schwerpunkt bezeichnet.^[2][3] In einem inhomogenen Feld ist dieser effektive Punkt verschieden vom Massenmittelpunkt und wird Gravizentrum genannt.^[4] In einem solchen Fall treten Gezeitenkräfte auf.^[5]

Der Begriff Massenmittelpunkt im Vergleich zum Volumenschwerpunkt

Ist ein Körper homogen (besteht er also aus einem Material, das überall die gleiche Dichte hat), so fällt sein Massenmittelpunkt mit seinem geometrischen Schwerpunkt zusammen. Besteht der Körper aus Teilen verschiedener Dichte, kann der Massenmittelpunkt vom Volumenschwerpunkt abweichen. Wenn die Verteilung der Masse innerhalb des Körpers bekannt ist, kann der Massenmittelpunkt durch Integration berechnet werden. Dies war der Anlass, der Isaac Newton zur Entwicklung der Infinitesimalrechnung führte (gleichzeitig mit Leibniz).

Bestimmung des Massenmittelpunktes

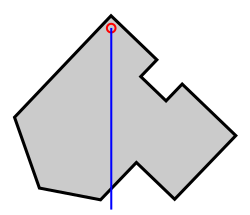
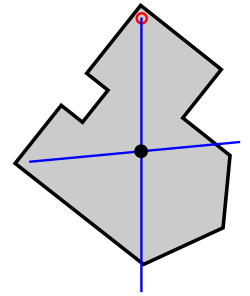
Aus den obigen Ausführungen gelangt man zu einem einfachen Verfahren zur annähernden Bestimmung des Massenmittelpunktes eines beliebigen starren Körpers. Dabei besteht die Näherung darin, die Abweichungen von Gravizentrum und Massenmittelpunkt und damit auch die Veränderungen der Lage des Gravizentrums bei Drehung des Körpers unberücksichtigt zu lassen: Hängt man den Körper an einem beliebigen Punkt auf, so liegt (in Ruhe) der (näherungsweise) Massenmittelpunkt auf der lotrechten Linie (= „Schwerlinie“) durch den Aufhängepunkt (blaue Linie im Bild rechts).

Wiederholt man dies mit einem anderen Aufhängepunkt, so findet man (näherungsweise) den Massenmittelpunkt als Schnittpunkt zweier solcher Geraden („Schwerlinien“). Dass ein solcher Schnittpunkt tatsächlich existiert und unabhängig von der Wahl der Aufhängepunkte ist, ist allerdings weniger trivial, als der erste Anschein glauben lässt.

Verblüffend ist die folgende Methode zur Bestimmung des Massenmittelpunktes eines schmalen und länglichen Gegenstandes (zum Beispiel Lineal oder Besen): Man lege den Gegenstand quer über die beiden auf gleicher Höhe nach vorne ausgestreckten Zeigefinger, was leicht möglich ist, solange die Finger noch weit voneinander entfernt sind. Nun bringe man langsam die Zeigefinger näher zueinander, bis sie sich berühren, wobei man sie stets auf möglichst gleicher Höhe hält. Sofern man dies langsam genug macht, gleitet der Gegenstand langsam über die Finger, ohne nach einer Seite zu kippen. Auf dem Finger, der dem Massenmittelpunkt näher liegt, lastet jeweils ein stärkerer Druck, was zu einer stärkeren Reibung führt. Das heißt, der Gegenstand gleitet vornehmlich über den anderen Finger. Hierdurch regelt sich das System so ein, dass bei beiden Fingern in etwa dieselbe Reibung vorliegt und der Massenmittelpunkt sich in ihrer Mitte befindet. Schließlich berühren sich also die Zeigefinger, der Gegenstand liegt nach wie vor waagerecht und der Schwerpunkt liegt über den beiden Fingern. Ist der Gegenstand allerdings zu sehr gebogen, ergibt sich der oben erwähnte Effekt und der Schwerpunkt liegt unterhalb des Unterstützungspunktes.

Siehe auch

• Massenverteilung
• Massenlinie (Verfahren)

Literatur

• Die Physik: ein Lexikon der gesamten Schulphysik. Schülerduden, Bibliographisches Institut, Mannheim 1974, ISBN 3-411-01122-X, S. 367–368.

Einzelnachweise

1. ↑ D. Gross, W. Hauger, J. Schröder, und W.A. Wall: Technische Mechanik 1: Statik. Springer-Lehrbuch 2011, ISBN 9783642138058, S. 114.
2. ↑ John McLester, Peter St. Pierre: Applied biomechanics: concepts and connections. Cengage Learning, 2008, ISBN 978-0-495-10586-2, S. 28.
3. ↑ John Harris, Walter Benenson, Horst Stöcker: Handbook of physics. Springer, 2002, ISBN 978-0-387-95269-7, S. 94.
4. ↑ Theo Koupelis, Karl F. Kuhn: In quest of the universe. Jones & Bartlett Learning, 13 April 2007, ISBN 978-0-7637-4387-1, S. 86.
5. ↑ Philip Ball: Life's matrix: a biography of water. University of California Press, 2001, ISBN 978-0-520-23008-8, S. 37.